题目内容
设a=20.4，b=log20.4，则a，b的大小关系为（ ）
| A、a＞b | B、b＞a |
| C、a=b | D、不能确定 |
考点：对数的运算性质
专题：函数的性质及应用
分析：利用指数函数和对数函数的单调性即可得出．
解答：
解：∵a=20.4＞20=1，b=log20.4＜log21=0，
∴a＞b．
故选：A．
∴a＞b．
故选：A．
点评：本题考查了指数函数和对数函数的单调性，属于基础题．
练习册系列答案
相关题目
设变量z，y满足约束条件
，则目标函数z=
的最大值为（ ）
|
| y |
| x |
A、
| ||
| B、3 | ||
| C、6 | ||
| D、9 |
设全集U={3，4，5，6}，集合A={3，5}，则∁UA=（ ）
| A、{4，5} | B、{6} |
| C、{4，6} | D、{3} |
若复数z满足zi=4-5i（其中i为虚数单位），则复数z为（ ）
| A、5-4i | B、-5+4i |
| C、5+4i | D、-5-4i |
已知函数y=
(-1＜x＜1)，则函数的值域为（ ）
| x-1 |
| x+1 |
| A、{y|y＜0} |
| B、{y|-1＜y＜0} |
| C、{y|y＞0} |
| D、{y|y≠1} |
将1，2，3，4四个数分为两组，每组至少一个数，则两组数的和相等的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
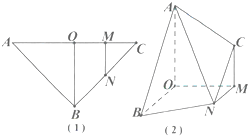如图（1），在三角形ABC中，BA=BC=2
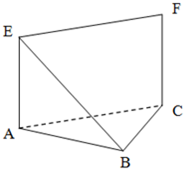如图，等腰直角△ABC中，∠ABC=90°，EA⊥平面ABC，FC∥EA，EA=FC=AB=a．