题目内容
已知数列{an},{bn}满足a1=3,anbn=2,bn+1=an(bn-
),n∈N*.
(1)求证:数列{
}是等差数列,并求数列{bn}的通项公式;
(2)设数列{cn}满足cn=2an-5,对于任意给定的正整数p,是否存在正整数q,r(p<q<r),使得
,
,
成等差数列?若存在,试用p表示q,r;若不存在,说明理由.
| 2 |
| 1+an |
(1)求证:数列{
| 1 |
| bn |
(2)设数列{cn}满足cn=2an-5,对于任意给定的正整数p,是否存在正整数q,r(p<q<r),使得
| 1 |
| cp |
| 1 |
| cq |
| 1 |
| cr |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件推导出bn+1=anbn-
=
,由此能证明{
}是等差数列,并能求出数列{bn}的通项公式.
(2)由an=n+2,得以cn=2an-5=2n-1,由此推导出当p=1时,不存在q,r满足题设条件;当p≥2时,存在q=2p-1,r=4p2-5p+2,满足题设条件.
| 2an |
| 1+an |
| 2bn |
| bn+2 |
| 1 |
| bn |
(2)由an=n+2,得以cn=2an-5=2n-1,由此推导出当p=1时,不存在q,r满足题设条件;当p≥2时,存在q=2p-1,r=4p2-5p+2,满足题设条件.
解答:
(1)证明:∵anbn=2,∴an=
,
则bn+1=anbn-
=2-
=2-
=
,…(2分)
∴
=
+
,
又a1=3,∴b1=
,
∴{
}是首项为
,公差为
的等差数列,…(4分)
即
=
+(n-1)×
=
,∴bn=
.…(6分)
(2)解:由(1)知an=n+2,∴cn=2an-5=2n-1,
①当p=1时,cp=c1=1,cq=2q-1,cr=2r-1,
若
,
,
成等差数列,则
=1+
(*),
∵p<q<r,∴q≥2,r≥3,
<1,1+
>1,
∴(*)不成立.…(9分)
②当p≥2时,若
,
,
成等差数列,
则
=
+
,
∴
=
-
=
,
即2r-1=
,∴r=
,…(12分)
欲满足题设条件,只需q=2p-1,此时r=4p2-5p+2,…(14分)
∵p≥2,∴q=2p-1>p,r-q=4p2-7p+3=4(p-1)2+p-1>0,
即r>q. …(15分)
综上所述,当p=1时,不存在q,r满足题设条件;
当p≥2时,存在q=2p-1,r=4p2-5p+2,满足题设条件.…(16分)
| 2 |
| bn |
则bn+1=anbn-
| 2an |
| 1+an |
=2-
| ||
1+
|
=2-
| 4 |
| bn+2 |
=
| 2bn |
| bn+2 |
∴
| 1 |
| bn+1 |
| 1 |
| bn |
| 1 |
| 2 |
又a1=3,∴b1=
| 2 |
| 3 |
∴{
| 1 |
| bn |
| 3 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| bn |
| 3 |
| 2 |
| 1 |
| 2 |
| n+2 |
| 2 |
| 2 |
| n+2 |
(2)解:由(1)知an=n+2,∴cn=2an-5=2n-1,
①当p=1时,cp=c1=1,cq=2q-1,cr=2r-1,
若
| 1 |
| cp |
| 1 |
| cq |
| 1 |
| cr |
| 2 |
| 2q-1 |
| 1 |
| 2r-1 |
∵p<q<r,∴q≥2,r≥3,
| 2 |
| 2q-1 |
| 1 |
| 2r-1 |
∴(*)不成立.…(9分)
②当p≥2时,若
| 1 |
| cp |
| 1 |
| cq |
| 1 |
| cr |
则
| 2 |
| 2q-1 |
| 1 |
| 2p-1 |
| 1 |
| 2r-1 |
∴
| 1 |
| 2r-1 |
| 2 |
| 2q-1 |
| 1 |
| 2p-1 |
| 4p-2q-1 |
| (2p-1)(2q-1) |
即2r-1=
| (2p-1)(2q-1) |
| 4q-2p-1 |
| 2pq+p-2q |
| 4p-2q-1 |
欲满足题设条件,只需q=2p-1,此时r=4p2-5p+2,…(14分)
∵p≥2,∴q=2p-1>p,r-q=4p2-7p+3=4(p-1)2+p-1>0,
即r>q. …(15分)
综上所述,当p=1时,不存在q,r满足题设条件;
当p≥2时,存在q=2p-1,r=4p2-5p+2,满足题设条件.…(16分)
点评:本题考查等差数列的证明,考查数列的通项公式的求法,考查使得数列为等差数列的正整数是否存在的判断,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
已知函数y=
(-1<x<1),则函数的值域为( )
| x-1 |
| x+1 |
| A、{y|y<0} |
| B、{y|-1<y<0} |
| C、{y|y>0} |
| D、{y|y≠1} |
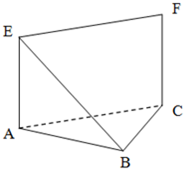 如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.
如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a. 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2 (理)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AB=AC=1,∠ABC=
(理)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AB=AC=1,∠ABC=