题目内容
设函数f(x)=ax2+(b-2)x+3(a≠0),若不等式f(x)>0的解集为(-1,3).
(1)求a,b的值;
(2)若函数f(x)在x∈[m,1]上的最小值为3,求实数m的值.
(1)求a,b的值;
(2)若函数f(x)在x∈[m,1]上的最小值为3,求实数m的值.
考点:二次函数在闭区间上的最值,二次函数的性质
专题:综合题
分析:第(1)问考查二次函数、一元二次方程、一元二次不等式三个二次的关系,根据不等式的解集知道对应方程的两个根,然后利用根与系数的关系求出a,b的值;第(2)问考查二次函数在闭区间上的最值,要分析对称轴与区间的关系.
解答:
解:(1)∵f(x)=ax2+(b-2)x+3>0的解集为(-1,3),
∴方程ax2+(b-2)x+3=0的两根为-1,3,
由根与系数的关系得,-1+3=-
,-1×3=
,解得a=-1,b=4;
(2)由(1)知,f(x)=-x2+2x+3,对称轴为x=1,
所以函数f(x)=-x2+2x+3在区间[m,1]上是增函数,
∴fmin(x)=f(m)=-m2+2m+3
由-m2+2m+3=3解得m=0或m=2,
根据题意知m<1,
∴m=0.
∴方程ax2+(b-2)x+3=0的两根为-1,3,
由根与系数的关系得,-1+3=-
| 2-b |
| a |
| 3 |
| a |
(2)由(1)知,f(x)=-x2+2x+3,对称轴为x=1,
所以函数f(x)=-x2+2x+3在区间[m,1]上是增函数,
∴fmin(x)=f(m)=-m2+2m+3
由-m2+2m+3=3解得m=0或m=2,
根据题意知m<1,
∴m=0.
点评:这是一三个二次的综合问题,主要考查三个二次的关系,二次函数在闭区间上的最值问题,考查了数形结合、方程的思想.

练习册系列答案
相关题目
设全集U={3,4,5,6},集合A={3,5},则∁UA=( )
| A、{4,5} | B、{6} |
| C、{4,6} | D、{3} |
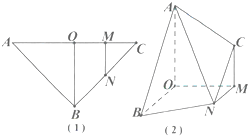 如图(1),在三角形ABC中,BA=BC=2
如图(1),在三角形ABC中,BA=BC=2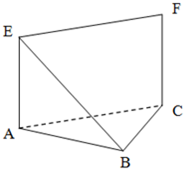 如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.
如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a. (理)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AB=AC=1,∠ABC=
(理)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AB=AC=1,∠ABC=