题目内容
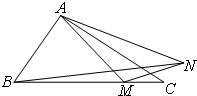 如图,已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°,
如图,已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°,| AM |
| AN |
(1)若
| AN |
| AC |
(2)求△ABN面积的最大值.
考点:正弦定理
专题:综合题,解三角形
分析:(1)利用△ABC的面积等于△ABM与△ACM面积的和,求出AM,利用∠MAN=30°,
•
=3,求出AN,利用余弦定理,计算BN的长;
(2)表示出△ABN面积,利用辅助角公式化简,即可求△ABN面积的最大值.
| AM |
| AN |
(2)表示出△ABN面积,利用辅助角公式化简,即可求△ABN面积的最大值.
解答:
解:(1)由
=λ
(λ>0),得点N在射线AC上,∠BAM=90°,
因为△ABC的面积等于△ABM与△ACM面积的和,
所以
AB•AM+
AC•AM•sin30°=
AB•ACsin120°,得:AM=
,…(3分)
又∠MAN=30°,
•
=3,
所以AM•ANcos30°=3,即AN=4,
所以BN=
=
,即BN=
;…(6分)
(2)设∠BAM=x,则∠CAM=120°-x,
因为△ABC的面积等于△ABM与△ACM面积的和,
所以
AB•AMsinx+
AC•AM•sin(120°-x)=
AB•ACsin120°,
得:AM=
,…(7分)
又∠MAN=30°,
•
=3,
所以AM•ANcos30°=3,即AN=4sinx+2
cosx,
所以△ABN的面积S=
(4sinx+2
cosx)sin(x+30°)
=
sin2x-
cos2x+
=
sin(2x-φ)+
…(10分)
(其中:sinφ=
,cosφ=
,φ,为锐角),
所以当2x-φ=90°时,△ABN的面积最大,最大值是
+
.…(12分)
| AN |
| AC |
因为△ABC的面积等于△ABM与△ACM面积的和,
所以
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
又∠MAN=30°,
| AM |
| AN |
所以AM•ANcos30°=3,即AN=4,
所以BN=
| 1+16-2×1×4cos120° |
| 21 |
| 21 |
(2)设∠BAM=x,则∠CAM=120°-x,
因为△ABC的面积等于△ABM与△ACM面积的和,
所以
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
得:AM=
| ||
2(sinx+
|
又∠MAN=30°,
| AM |
| AN |
所以AM•ANcos30°=3,即AN=4sinx+2
| 3 |
所以△ABN的面积S=
| 1 |
| 2 |
| 3 |
=
| 5 |
| 4 |
| ||
| 4 |
3
| ||
| 4 |
2
| ||
| 4 |
3
| ||
| 4 |
(其中:sinφ=
| ||
2
|
| 5 | ||
2
|
所以当2x-φ=90°时,△ABN的面积最大,最大值是
2
| ||
| 4 |
3
| ||
| 4 |
点评:本题考查正弦、余弦定理的运用,考查三角形面积的计算,考查辅助角公式,考查学生的计算能力,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
若复数z满足zi=4-5i(其中i为虚数单位),则复数z为( )
| A、5-4i | B、-5+4i |
| C、5+4i | D、-5-4i |
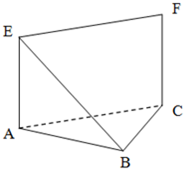 如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.
如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.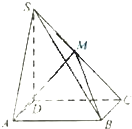 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=