题目内容
已知直线l与圆C:x2+y2+2x-4y+a=0相交于A,B两点,弦AB的中点为M(0,1).
(1)实数a的取值范围以及直线l方程
(2)若弦AB=2
,求圆的方程.
(1)实数a的取值范围以及直线l方程
(2)若弦AB=2
| 7 |
考点:直线和圆的方程的应用,圆的标准方程
专题:直线与圆
分析:(1)利用配方法得到圆的标准方程,根据直线,点与圆的位置关系即可求出a的取值范围.
(2)求出圆心到直线的距离,根据弦AB=2
,求出圆的半径,即可得到圆的方程.
(2)求出圆心到直线的距离,根据弦AB=2
| 7 |
解答:
解:(1)圆的标准方程为(x+1)2+(y-2)2=5-a,
则圆心C(-1,2),半径r=
,
∵弦AB的中点为M(0,1).
∴点M在圆内部,即
<
,
即
<
,
∴5-a>2,即a<3.
∵弦的中点为M(0,1).
∴直线CM的斜率k=
=-1,
则直线l的斜率k=1,
则直线l的方程为y-1=x,即x-y+1=0.
(2)圆心C到直线x-y+1=0的距离d=
=
=
,
若弦AB=2
,
则d 2+(
)2=r2,
即2+7=5-a=9,
解得a=-4,此时半径r=3,
∴圆的标准方程为(x+1)2+(y-2)2=9.
则圆心C(-1,2),半径r=
| 5-a |
∵弦AB的中点为M(0,1).
∴点M在圆内部,即
| 12+(1-2)2 |
| 5-a |
即
| 2 |
| 5-a |
∴5-a>2,即a<3.
∵弦的中点为M(0,1).
∴直线CM的斜率k=
| 2-1 |
| -1-0 |
则直线l的斜率k=1,
则直线l的方程为y-1=x,即x-y+1=0.
(2)圆心C到直线x-y+1=0的距离d=
| |-1-2+1| | ||
|
| 2 | ||
|
| 2 |
若弦AB=2
| 7 |
则d 2+(
| AB |
| 2 |
即2+7=5-a=9,
解得a=-4,此时半径r=3,
∴圆的标准方程为(x+1)2+(y-2)2=9.
点评:本题主要考查直线和圆的方程的应用,利用配方法将圆配成标准方程是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
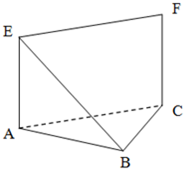 如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.
如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a. 三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.
三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.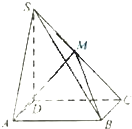 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=