��Ŀ����
3��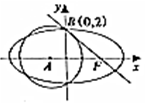 ��ͼ����FΪ��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���ҽ��㣬ԲA����x-t��2+y2=$\frac{16}{3}$��t��0������ԲC��һ��������ΪB��0��2������ֱ��FB��ԲA�����ڵ�B��
��ͼ����FΪ��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���ҽ��㣬ԲA����x-t��2+y2=$\frac{16}{3}$��t��0������ԲC��һ��������ΪB��0��2������ֱ��FB��ԲA�����ڵ�B��������t��ֵ����ԲC�ı����̣�
������F������ԲC���㣬��P����ԲC�ϳ����������������������һ�㣬�ҡ�F��PF=�ȣ���ȵ����ֵ��
���� ����������֪b=2���ɴ�����${t}^{2}+4=\frac{16}{3}$�������t���ɶ����ɶ������c=2$\sqrt{3}$��a=4���ɴ��������ԲC�ı����̣�
������|PF��|=m��|PF|=n�������Ҷ�����cos��=$\frac{2{b}^{2}}{mn}-1$��$\frac{2{b}^{2}}{��\frac{m+n}{2}��^{2}}$-1���ɴ������cos�ȵ���СֵΪ-$\frac{1}{2}$���ȵ����ֵΪ120�㣮
��� �⣺����������֪b=2��
��${t}^{2}+4=\frac{16}{3}$�����t2=$\frac{4}{3}$��
��t��0����t=-$\frac{2\sqrt{3}}{3}$��
��Rt��AFB��|AB|2+|FB|2=|AF|2����$\frac{16}{3}+��4+c��^{2}=��\frac{2\sqrt{3}}{3}+c��^{2}$��
���c=2$\sqrt{3}$��a=4��
����ԲC�ı�����Ϊ$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1$��
������|PF��|=m��|PF|=n��
�������Ҷ����ã�
cos��=$\frac{{m}^{2}+{n}^{2}-��2c��^{2}}{2mn}$=$\frac{��m+n��^{2}-2mn-��2c��^{2}}{2mn}$
=$\frac{��2a��^{2}-2mn-��2c��^{2}}{2mn}$=$\frac{4{b}^{2}}{2mn}-1$=$\frac{2{b}^{2}}{mn}-1$��$\frac{2{b}^{2}}{��\frac{m+n}{2}��^{2}}$-1��
��cos$�ȡ�\frac{2{b}^{2}}{{a}^{2}}$-1����cos��$��\frac{8}{16}-1=-\frac{1}{2}$��
���ҽ���m=n=4ʱ��ȡ�Ⱥţ�
��cos�ȵ���СֵΪ-$\frac{1}{2}$���ȵ����ֵΪ120�㣮
���� ���⿼����Բ���̵�������ǵ����ֵ�������е��⣬����ʱҪ�������⣬ע����Բ���ʡ����Ҷ����ĺ������ã�

 ��У����ϵ�д�
��У����ϵ�д�| A�� | ��-$\frac{1}{2}$��$\frac{3}{2}$�� | B�� | ��-�ޣ�$\frac{3}{2}$�� | C�� | ��$\frac{3}{2}$��+�ޣ� | D�� | ��-�ޣ�$-\frac{1}{2}$���ȣ�$\frac{3}{2}$��+�ޣ� |

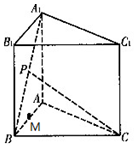 ��֪��������ABC-A1B1C�ĸ����ⳤ��Ϊa��PΪA1B���е㣬MΪAB���е㣬
��֪��������ABC-A1B1C�ĸ����ⳤ��Ϊa��PΪA1B���е㣬MΪAB���е㣬