题目内容
已知等差数列{an}中，a1+a2+a3+a4+a5=100，则a3=（ ）
| A、10 | B、20 | C、30 | D、40 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：因为a1+a5=a2+a4=2a3，所以由a1+a2+a3+a4+a5=100得5a3=100，故a3=20．
解答：
解：在等差数列中，
∵a1+a5=a2+a4=2a3，
∴由a1+a2+a3+a4+a5=100得5a3=100，
∴a3=20．
故选B．
∵a1+a5=a2+a4=2a3，
∴由a1+a2+a3+a4+a5=100得5a3=100，
∴a3=20．
故选B．
点评：本题考查数列的性质和应用，解题时要注意公式的灵活运用．
练习册系列答案
科学实验活动册系列答案
相关题目
把函数y=sin（2x+
）的图象向左平移
个单位，再把图象上所有的点的横坐标扩大为原来的2倍，纵坐标缩短为原来的
倍；然后把图象向下平移2个单位．最后得到的函数解析式为：（ ）
| π |
| 3 |
| π |
| 12 |
| 1 |
| 3 |
A、y=
| ||||
| B、y=3cos4x+2 | ||||
C、y=
| ||||
D、y=3sin（4x+
|
若函数f（x）=|x2-k|的图象与函数g（x）=x-3的图象至多有一个公共点，则实数k的取值范围是（ ）
| A、（-∞，3] |
| B、[9，+∞） |
| C、（0，9] |
| D、（-∞，9] |
若函数f（x）=
在x=1处可导，则实数a和b的值分别是（ ）
|
| A、1和0 | B、2和-1 |
| C、1和-2 | D、0和1 |
已知Sn为等差数列{an}的前n项和，且满足a2+a2013=32，则log2
=（ ）
| S2014 |
| 2014 |
| A、6 | B、5 | C、4 | D、3 |
点A，B，C，D均在同一球面上，且AB、AC、AD两两垂直，且AB=1，AC=2，AD=3，则该球的表面积为（ ）
| A、7π | ||||
| B、14π | ||||
C、
| ||||
D、
|
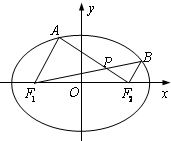如图，在平面直角坐标系xoy中，椭圆| x2 |
| 2 |
2
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
等比数列{an}前n项和为Sn，q=3，则
=（ ）
| S4 |
| a4 |
A、
| ||
B、
| ||
C、
| ||
D、
|