题目内容
设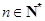 且
且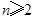 ,证明:
,证明:
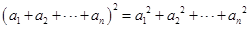
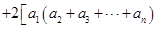
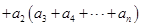
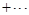
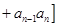 .
.
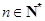 且
且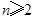 ,证明:
,证明: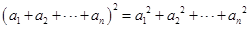
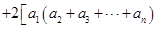
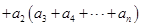
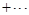
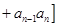 .
.运用数学归纳法来加以证明与自然数相关的命题。
试题分析:证明:(1)当
 时,有
时,有 ,命题成立. 2分
,命题成立. 2分(2)假设当
 时,命题成立,
时,命题成立,即




 成立, 4分
成立, 4分那么,当
 时,有
时,有









 .
.
 +
+



 .
.所以当
 时,命题也成立. 8分
时,命题也成立. 8分根据(1)和(2),可知结论对任意的
 且
且 都成立. 10分
都成立. 10分点评:主要是考查了数学归纳法的运用,证明命题,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
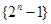 的前
的前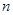 项组成集合
项组成集合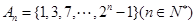 ,从集合
,从集合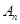 中任取
中任取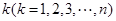 个数,其所有可能的
个数,其所有可能的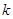 个数的乘积的和为
个数的乘积的和为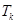 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记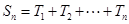 .例如:当
.例如:当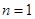 时,
时,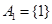 ,
,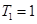 ,
,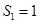 ;当
;当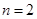 时,
时,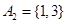 ,
,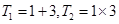 ,
,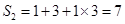 .
.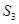 ;
;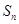 ,并用数学归纳法证明.
,并用数学归纳法证明. +
+ +…+
+…+ (n∈N*),用数学归纳法证明f(2n)>
(n∈N*),用数学归纳法证明f(2n)> 时,f(2k+1)-f(2k)等于________.
时,f(2k+1)-f(2k)等于________. +
+ +…+
+…+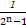 <n(n∈N*,n>1)时,第一步应验证的不等式是 .
<n(n∈N*,n>1)时,第一步应验证的不等式是 .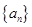 的前
的前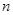 项和为
项和为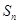 ,且对任意
,且对任意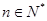 都有:
都有: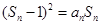 ;
;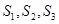 ;
;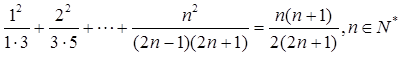
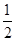 +
+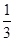 +…+
+…+ <n(n∈N*,n>1)时,在证明过程的第二步从n=k到n=k+1时,左边增加的项数是 ( )
<n(n∈N*,n>1)时,在证明过程的第二步从n=k到n=k+1时,左边增加的项数是 ( )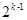
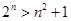 对于
对于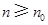 的自然数
的自然数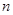 都成立”时,第一步证明中的起始值
都成立”时,第一步证明中的起始值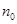 应取_____________.
应取_____________. (n∈N*),则f(k+1)-f(k)=________.
(n∈N*),则f(k+1)-f(k)=________.