题目内容
求证: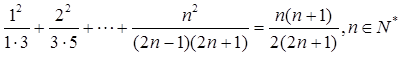
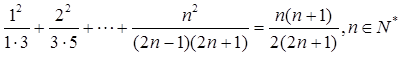
证明与自然数相关的命题一般可以采用数学归纳法来证明,分为两个步骤,来进行。
试题分析:证明(1)当
 时,左边=
时,左边= ,右边=
,右边= ,等式成立. 3分
,等式成立. 3分(2)假设当
 时,等式成立,即
时,等式成立,即 6分
6分那么,当
 时,
时,





这就是说,当
 时等式也成立. 13分
时等式也成立. 13分根据(1)和(2),可知等式对任何
 都成立. 14分
都成立. 14分点评:解决的关键是正确的运用数学归纳法的思想来对于命题加以证明,属于基础题。

练习册系列答案
相关题目
 x3-x,数列{an}满足条件:a1≥1,an+1≥f'(an+1).试比较
x3-x,数列{an}满足条件:a1≥1,an+1≥f'(an+1).试比较 +
+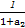 +
+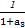 +…+
+…+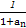 与1的大小,并说明理由.
与1的大小,并说明理由.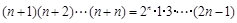 ,从
,从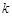 到
到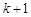 ,左边需要增乘的代数式为()
,左边需要增乘的代数式为()



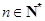 且
且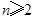 ,证明:
,证明: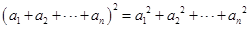
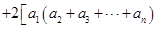
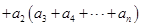
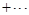
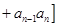 .
.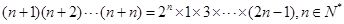 ”时,从“
”时,从“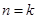 ”变到 “
”变到 “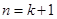 ”时,左边应增乘的因式是
”时,左边应增乘的因式是 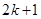
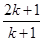

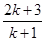
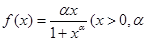 为常数,数列
为常数,数列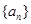 满足:
满足: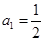 ,
,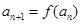 ,
,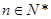 .
.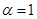 时,求数列
时,求数列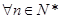 有:
有: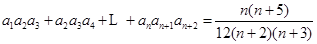 ;
;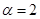 ,且对
,且对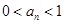 ,证明:
,证明: .
.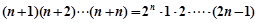 ”(
”(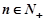 )时,从“
)时,从“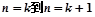 ”时,左边的式子之比是( )
”时,左边的式子之比是( )
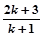
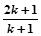
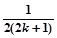
 ”,第一步在验证
”,第一步在验证 时,左边应取的式子是____.
时,左边应取的式子是____.