题目内容
19.已知数列{an}的前n项和为Sn,a1=1,Sn=3an+1,则an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{1}{3}×(\frac{4}{3})^{n-2},n≥2}\end{array}\right.$.分析 由Sn=3an+1,Sn-1=3an,则可得3an+1=4an.再利用等比数列的通项公式即可得出.
解答 解:当n=1时,a1=3a2,
∴a2=$\frac{1}{3}$
当n≥2时,
由Sn=3an+1,Sn-1=3an,
∴an=3an+1-3an,
∴3an+1=4an.
∴an+1=$\frac{4}{3}$an,
∴从第二项开始,数列{an}是$\frac{1}{3}$为首项,以$\frac{4}{3}$为公比的等比数列,
∴an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{1}{3}×(\frac{4}{3})^{n-2},n≥2}\end{array}\right.$
故答案为:$\left\{\begin{array}{l}{1,n=1}\\{\frac{1}{3}×(\frac{4}{3})^{n-2},n≥2}\end{array}\right.$
点评 本题考查了递推式的意义、等比数列的通项公式,属于基础题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
7.已知a,b∈R,i是虚数单位,若a-2bi与1+4i互为共轭复数,则|a+bi|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
4.设函数$f(x)=\sqrt{x-1}$,则$f(\frac{x}{2})+f(\frac{4}{x})$的定义域为( )
| A. | $[\frac{1}{2},4]$ | B. | [2,4] | C. | [1,+∞) | D. | [$\frac{1}{4}$,2] |
8.设集合A={x|x≤-4或x≥2},B={x||x-1|≤3},则等于∁R(A∩B)( )
| A. | [2,4] | B. | [-2,2) | C. | (-∞,2)∪(4,+∞) | D. | (-∞,-4)∪(-2,+∞) |
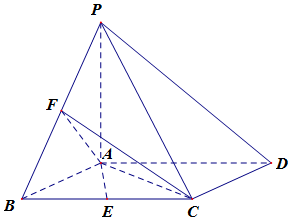 如图所示,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PB的中点.
如图所示,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PB的中点.