题目内容
设集合U=R，集合M={x|x＞1}，P={x|x2＞1}，则下列关系正确的是（ ）
| A、M=P |
| B、（∁UM）∩P=∅ |
| C、P⊆M |
| D、M⊆P |
考点：集合的包含关系判断及应用
专题：集合
分析：根据M={x|x＞1}，P={x|x2＞1}={x|x＞1或x＜-1}，利用集合间的包含关系的概念能够得到结果．
解答：
解：∵M={x|x＞1}，
P={x|x2＞1}={x|x＞1或x＜-1}，
∴M⊆P．
故选D．
P={x|x2＞1}={x|x＞1或x＜-1}，
∴M⊆P．
故选D．
点评：本题考查集合的包含关系的判断和应用，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目
已知正方体ABCD-A1B1C1D1的各棱长为2，则D1到面AB1C的距离为函数f（x）=3x-x3的单调递增区间是（ ）
| A、[-1，1] | ||||
| B、[1，+∞）∪（-∞，-1] | ||||
| C、[1，+∞）及（-∞，-1] | ||||
D、[-
|
已知正四棱锥O-ABCD中，OA=AB，则OA与底面ABCD所成角的正弦值等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
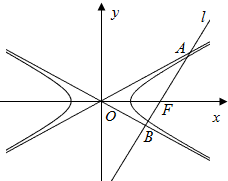如图所示，已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
| AF |
| FB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线
-
=1（a＞0，b＞0）的一条渐近线方程为x-2y=0，则该双曲线的离心率是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
三棱柱ABC-A1B1C1体积为V，M是AA1中点，求四棱锥M-BCC1B1的体积．