题目内容
3.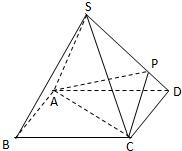 如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点,且SD⊥PC.
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点,且SD⊥PC.(1)求二面角P-AC-D的大小;
(2)在侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE:EC的值;若不存在,试说明理由.
分析 (1)连结BD,交AC于点O,连结SO,OP,设SD的中点为Q,连结BQ,△SBD为等边三角形,推导出∠POD是二面角P-AC-D的平面角,由此能求出二面角P-AC-D的大小.
(2)在平面SCD内作QE∥CP,则QE∥面PAC,从而BQ∥面PAC,进而面EBQ∥面PAC,由此能求出存在点E且SE:EC=2:1,使得BE∥面PAC.
解答 解:(1)连结BD,交AC于点O,连结SO,OP,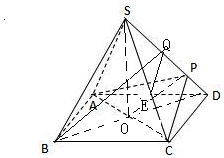
∵AC⊥平面SBD,∴OP⊥SD,
设SD的中点为Q,
连结BQ,△SBD为等边三角形,∴BQ⊥SD,
∴P为QD的中点,∴P为SD的四等分点,
PD=$\frac{1}{4}$SD,OD=$\frac{1}{2}$BD,
又∵AC⊥OP,AC⊥DO,
∴∠POD是二面角P-AC-D的平面角,
sin∠POD=$\frac{PD}{OD}$=$\frac{\frac{1}{4}SD}{\frac{1}{2}BD}$=$\frac{1}{2}$,
由图可知二面角P-AC-D为锐二面角,
∴二面角P-AC-D的大小为30°.
(2)存在点E且SE:EC=2:1,使得BE∥面PAC.
证明如下:
在平面SCD内作QE∥CP,∴QE∥面PAC,
又BQ∥OP,∴BQ∥面PAC,
又QE∩BQ=Q,∴面EBQ∥面PAC,
∵BE?面EBQ,∴BE∥面PAC,
∴SE:EC=SQ:QP=2:1.
点评 本题考查二面角的大小的求法,考查满足线面平行的点是否存在的求法与判断,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、转化化归思想,是中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
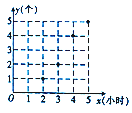 为确定加工某零件的时间,某工人做了四次实验,得到的数据的散点图如图所示.
为确定加工某零件的时间,某工人做了四次实验,得到的数据的散点图如图所示.