题目内容
14.二项式(x2+$\frac{2}{\sqrt{x}}$)5展开式中的常数项是80.分析 利用通项公式即可得出.
解答 解:二项式(x2+$\frac{2}{\sqrt{x}}$)5展开式中的通项公式:Tr+1=${∁}_{5}^{r}$(x2)5-r$(\frac{2}{\sqrt{x}})^{r}$=2r${∁}_{5}^{r}$${x}^{10-\frac{5r}{2}}$,
令10-$\frac{5r}{2}$=0,解得r=4.
∴常数项=${2}^{4}{∁}_{5}^{4}$=80.
故答案为:80.
点评 本题考查了二项式定理的通项公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
4.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的表面积为( )
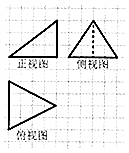

| A. | 20+3$\sqrt{2}$ | B. | 16+8$\sqrt{2}$ | C. | 18+3$\sqrt{5}$ | D. | 18+6$\sqrt{5}$ |
5.《九章算术》中有一个“两鼠穿墙”问题:今有垣(墙,读音)厚五尺,两鼠对穿,大鼠日穿(第一天挖)一尺,小鼠也日穿一尺.大鼠日自倍(以后每天加倍),小鼠日自半(以后每天减半).问何日(第几天)两鼠相逢( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.定义在R上的函数f(x)的图象关于y轴对称,且f(x)在[0,+∞)上单调递减,若关于x的不等式f(2mx-lnx-3)≥2f(3)-f(-2mx+lnx+3)在x∈[1,3]上恒成立,则实数m的取值范围为( )
| A. | [$\frac{1}{2e}$,$\frac{ln6+6}{6}$] | B. | [$\frac{1}{e}$,$\frac{ln6+6}{3}$] | C. | [$\frac{1}{e}$,$\frac{ln3+6}{3}$] | D. | [$\frac{1}{2e}$,$\frac{ln3+6}{6}$] |
4.已知x1,x2,…,xn的平均数为10,标准差为2,则2x1-1,2x2-1,…,2xn-1的平均数和标准差分别为( )
| A. | 19和2 | B. | 19和3 | C. | 19和4 | D. | 19和8 |
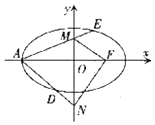 已知椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左顶点为A,右焦点为F,O为原点,M,N是y轴上的两个动点,且MF⊥NF,直线AM和AN分别与椭圆C交于E,D两点.
已知椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左顶点为A,右焦点为F,O为原点,M,N是y轴上的两个动点,且MF⊥NF,直线AM和AN分别与椭圆C交于E,D两点.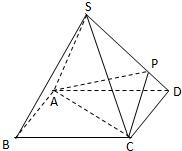 如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点,且SD⊥PC.
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点,且SD⊥PC.