题目内容
15.已知函数f(x)=-sin2x+msinx+2,当x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时函数有最大值为$\frac{3}{2}$,求此时m的值.分析 利用正弦函数的定义域和值域求得sinx的范围,再利用函数的最大值为$\frac{3}{2}$、二次函数的性质,分类讨论求得m的值.
解答 解:当x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,sinx∈[$\frac{1}{2}$,1],
函数f(x)=-sin2x+msinx+2=-${(sinx-\frac{m}{2})}^{2}$+$\frac{{m}^{2}}{4}$+2,
若$\frac{m}{2}$<$\frac{1}{2}$,即m<1,则当sinx=$\frac{1}{2}$时,函数取得最大值为-$\frac{1}{4}$+$\frac{1}{2}$m+2=$\frac{3}{2}$,∴m=-$\frac{1}{2}$.
若-$\frac{1}{2}$≤$\frac{m}{2}$≤1,即-1≤m≤2,则当sinx=$\frac{m}{2}$时,函数取得最大值为$\frac{{m}^{2}}{4}$+2=$\frac{3}{2}$,∴m无解.
若$\frac{m}{2}$>1,即m>2,则当sinx=1时,函数取得最大值为-1+m+2=$\frac{3}{2}$,∴m=$\frac{1}{2}$(不合题意,舍去).
综上,m=-$\frac{1}{2}$.
点评 本题主要考查正弦函数的定义域和值域,二次函数的性质,属于中档题.

练习册系列答案
相关题目
5.《九章算术》中有一个“两鼠穿墙”问题:今有垣(墙,读音)厚五尺,两鼠对穿,大鼠日穿(第一天挖)一尺,小鼠也日穿一尺.大鼠日自倍(以后每天加倍),小鼠日自半(以后每天减半).问何日(第几天)两鼠相逢( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.已知x1,x2,…,xn的平均数为10,标准差为2,则2x1-1,2x2-1,…,2xn-1的平均数和标准差分别为( )
| A. | 19和2 | B. | 19和3 | C. | 19和4 | D. | 19和8 |
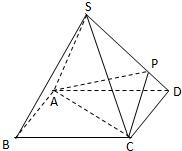 如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点,且SD⊥PC.
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点,且SD⊥PC.