题目内容
12.已知函数f(x)=lnx-x.(1)求f(x)的单调区间及最大值;
(2)若数列{an}的通项公式为${a_n}=1+\frac{1}{2^n}({n∈{N^*}})$,试结合(1)中有关结论证明:a1•a2•a3…an<e(e为自然对数的底数).
分析 (1)求出函数f(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最大值即可;
(2)根据ln x≤x-1,得到ln an=ln(1+$\frac{1}{2n}$)<$\frac{1}{2n}$,累加即可.
解答 (1)解:因f(x)=ln x-x,所以f′(x)=$\frac{1}{x}$-1=$\frac{1-x}{x}$.
当x∈(0,1)时,f′(x)>0;当x∈(1,+∞)时,f′(x)<0.
所以f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞);
f(x)的最大值为-1…(6分)
(2)证明:由(1)知,当x>0时,f(x)≤f(1)=-1,
即ln x≤x-1.当且仅当x=1时才能取等号.
因为an=1+$\frac{1}{2n}$(n∈N*),an大于零且不等于1,
所以ln an=ln(1+$\frac{1}{2n}$)<$\frac{1}{2n}$.
令k=1,2,3,…+,n,这n个式子相加得:
ln a1+ln a2+…+ln an<$\frac{1}{2}$+$\frac{1}{22}$+$\frac{1}{23}$+…$\frac{1}{2n}$=1-$\frac{1}{2n}$<1.
即ln (a1a2a3…+an)<1,所以a1a2a3…an<e…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道中档题.

练习册系列答案
相关题目
4.已知x1,x2,…,xn的平均数为10,标准差为2,则2x1-1,2x2-1,…,2xn-1的平均数和标准差分别为( )
| A. | 19和2 | B. | 19和3 | C. | 19和4 | D. | 19和8 |
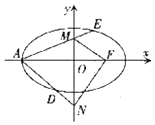 已知椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左顶点为A,右焦点为F,O为原点,M,N是y轴上的两个动点,且MF⊥NF,直线AM和AN分别与椭圆C交于E,D两点.
已知椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左顶点为A,右焦点为F,O为原点,M,N是y轴上的两个动点,且MF⊥NF,直线AM和AN分别与椭圆C交于E,D两点.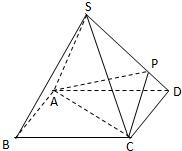 如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点,且SD⊥PC.
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点,且SD⊥PC.