题目内容
18．已知函数f（x）=$\left\{\begin{array}{l}{|lo{g}_{2}（x+1）|，x∈（-1，3）}\\{\frac{4}{x-1}，x∈[3，+∞）}\end{array}\right.$则函数g（x）=f[f（x）]-1的零点个数为（ ）| A． | 1 | B． | 3 | C． | 4 | D． | 6 |
分析 令f（x）令f（x）=1得x1=-$\frac{1}{2}$，x2=1，x3=5，再画出f（x）的图象，结合图象可得答案．
解答 解：令f（x）=1得x1=-$\frac{1}{2}$，x2=1，x3=5，
令g（x）=f[f（x）]-1=0，
作出图象如图所示：
由图象可得当f（x）=-$\frac{1}{2}$无解，
f（x）=1有3个解，
f（x）=5有1个解，
综上所述函数g（x）=f[f（x）]-1的零点个数为4，
故选：C
点评 本题考查了函数零点的问题，以及分段函数的问题，属于中档题
练习册系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
9．定义在R上的函数f（x）的图象关于y轴对称，且f（x）在[0，+∞）上单调递减，若关于x的不等式f（2mx-lnx-3）≥2f（3）-f（-2mx+lnx+3）在x∈[1，3]上恒成立，则实数m的取值范围为（ ）
| A． | [$\frac{1}{2e}$，$\frac{ln6+6}{6}$] | B． | [$\frac{1}{e}$，$\frac{ln6+6}{3}$] | C． | [$\frac{1}{e}$，$\frac{ln3+6}{3}$] | D． | [$\frac{1}{2e}$，$\frac{ln3+6}{6}$] |
如图，在四棱锥P-ABCD中，平面PAB⊥平面ABCD，AD∥BC，PA⊥AB，CD⊥AD，BC=CD=$\frac{1}{2}$AD，E为AD的中点．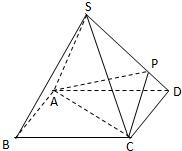
如图，四棱锥S-ABCD的底面是正方形，每条侧棱的长都是底面边长的$\sqrt{2}$倍，P为侧棱SD上的点，且SD⊥PC．