题目内容
8.已知点P为圆x2+y2=25上一动点,若点P由点(3,4)逆时针旋转45°到达Q点,则点Q的坐标为(-$\frac{\sqrt{2}}{2}$,$\frac{7\sqrt{2}}{2}$).分析 由已知,点Q到坐标原点O的距离等于圆的半径5,且∠QOx=α+45°,再由任意角的三角函数公式计算可得.
解答 解:由题意,cosα=$\frac{3}{5}$,sinα=$\frac{4}{5}$,
∴cos(α+45°)=$\frac{3}{5}$×$\frac{\sqrt{2}}{2}$-$\frac{4}{5}×\frac{\sqrt{2}}{2}$=-$\frac{\sqrt{2}}{10}$,sin(α+45°)=$\frac{7\sqrt{2}}{10}$.
∴Q(-$\frac{\sqrt{2}}{2}$,$\frac{7\sqrt{2}}{2}$).
故答案为:(-$\frac{\sqrt{2}}{2}$,$\frac{7\sqrt{2}}{2}$).
点评 本题考查点的坐标的计算,用到了任意角的三角函数公式的变形公式.是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
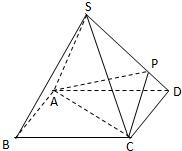 如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点,且SD⊥PC.
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点,且SD⊥PC.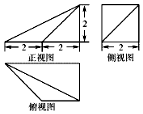
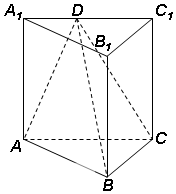 已知在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC⊥BC,BC=C1C=$\frac{1}{2}AC$=1,D是A1C1上的一点,且C1D=kA1C1.
已知在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC⊥BC,BC=C1C=$\frac{1}{2}AC$=1,D是A1C1上的一点,且C1D=kA1C1.