题目内容
8.一个扇形的圆心角为$\frac{2π}{3}$,半径为$\sqrt{3}$,则此扇形的面积为( )| A. | π | B. | $\frac{5π}{4}$ | C. | $\frac{{\sqrt{3}π}}{3}$ | D. | $\frac{{2\sqrt{3}}}{9}{π^2}$ |
分析 利用扇形的面积公式可求扇形的面积.
解答 解:∵扇形的圆心角为$\frac{2π}{3}$,半径为$\sqrt{3}$,
∴扇形的面积S=$\frac{1}{2}×$($\sqrt{3}$)2×$\frac{2π}{3}$=π.
故选:A.
点评 本题考查扇形的弧长与面积公式,正确运用公式是解题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.函数f(x)在定义域R内可导,若f(x+1)是偶函数,且(x-1)f'(x)<0,设a=f(0),$b=f(\frac{1}{2})$,c=f(3),则( )
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<c<a |
19.随机采访50名观众对某电视节目的满意度,得到如下列联表:单位:人
附表和公式如下:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d为样本容量.根据以上数据可知( )
| 满意 | 不满意 | 合计 | |
| 男 | 10 | 20 | 30 |
| 女 | 15 | 5 | 20 |
| 合计 | 25 | 25 | 50 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
| A. | 有95%的把握认为对电视节目的满意度与性别无关 | |
| B. | 有99%的把握认为对电视节目的满意度与性别无关 | |
| C. | 有99%的把握认为对电视节目的满意度与性别有关 | |
| D. | 有95%的把握认为对电视节目的满意度与性别有关 |
16.已知△ABC的三个顶点A、B、C及平面内一点P,若$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{AC}$,则点P在( )
| A. | △ABC的内部 | B. | △ABC的外部 | C. | P在线段AC上 | D. | P在线段AB上 |
3.若△ABC的内角A,B,C的对边分别为a,b,c,已知2bsin2A=asinB,且c=2b,则$\frac{a}{b}$=( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
13.若函数f(x)=ax+loga(x2+1)在[1,2]上的最大值与最小值之和为a2+a+2,则实数a的值是( )
| A. | $\sqrt{10}$ | B. | 10 | C. | $\sqrt{2}$ | D. | 2 |
20.已知一个算法:
(1)m=a.
(2)如果b<m,则m=b,输出m;否则执行第3步.
(3)如果c<m,则m=c,输出m.
如果a=3,b=6,c=2,
那么执行这个算法的结果是( )
(1)m=a.
(2)如果b<m,则m=b,输出m;否则执行第3步.
(3)如果c<m,则m=c,输出m.
如果a=3,b=6,c=2,
那么执行这个算法的结果是( )
| A. | 3 | B. | 6 | C. | 2 | D. | m |
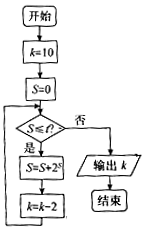
18.某程序框图如图所示,若t=7,则输出的值为( )

| A. | 8 | B. | 6 | C. | 4 | D. | 2 |