题目内容
19.随机采访50名观众对某电视节目的满意度,得到如下列联表:单位:人| 满意 | 不满意 | 合计 | |
| 男 | 10 | 20 | 30 |
| 女 | 15 | 5 | 20 |
| 合计 | 25 | 25 | 50 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
| A. | 有95%的把握认为对电视节目的满意度与性别无关 | |
| B. | 有99%的把握认为对电视节目的满意度与性别无关 | |
| C. | 有99%的把握认为对电视节目的满意度与性别有关 | |
| D. | 有95%的把握认为对电视节目的满意度与性别有关 |
分析 根据条件中所给的观测值,同题目中节选的观测值表进行检验,得到观测值对应的结果,得到结论有99%以上的把握认为“爱好该项运动与性别有关”.
解答 解:K2=$\frac{50(10×5-20×15)^{2}}{25×25×30×20}$≈8.333>6.635,
∴这个结论有0.010的机会出错,
即有99%的把握认为对电视节目的满意度与性别有关,
故选:C.
点评 本题考查了独立性检验的应用问题,也考查了对观测值表的认识与应用,是基础题目.

练习册系列答案
相关题目
8.一个扇形的圆心角为$\frac{2π}{3}$,半径为$\sqrt{3}$,则此扇形的面积为( )
| A. | π | B. | $\frac{5π}{4}$ | C. | $\frac{{\sqrt{3}π}}{3}$ | D. | $\frac{{2\sqrt{3}}}{9}{π^2}$ |
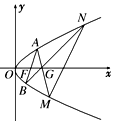 如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).
如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).