题目内容
16.已知△ABC的三个顶点A、B、C及平面内一点P,若$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{AC}$,则点P在( )| A. | △ABC的内部 | B. | △ABC的外部 | C. | P在线段AC上 | D. | P在线段AB上 |
分析 根据$\overrightarrow{AC}$=$\overrightarrow{PC}-\overrightarrow{PA}$可得$\overrightarrow{PB}$=-2$\overrightarrow{PA}$,从而得出P为AB的三等分点.
解答 解:∵$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{AC}$=$\overrightarrow{PC}$-$\overrightarrow{PA}$,
∴2$\overrightarrow{PA}$+$\overrightarrow{PB}$=0,即$\overrightarrow{PB}$=-2$\overrightarrow{PA}$,
∴P在线段AB上.
故选D.
点评 本题考查了平面向量的几何运算,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.某三棱锥的三视图如图所示,则该三棱锥的体积是( )


| A. | 2 | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
8.一个扇形的圆心角为$\frac{2π}{3}$,半径为$\sqrt{3}$,则此扇形的面积为( )
| A. | π | B. | $\frac{5π}{4}$ | C. | $\frac{{\sqrt{3}π}}{3}$ | D. | $\frac{{2\sqrt{3}}}{9}{π^2}$ |
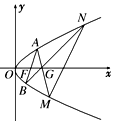 如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).
如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).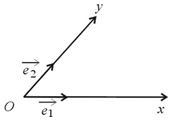 如图,设ox,oy是平面内相交成θ°的两条数轴,$\overrightarrow{e_1}$,$\overrightarrow{e_2}$分别是与ox,oy正方向同向的单位向量,若向量$\overrightarrow{op}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则把有序实数对(x,y)叫做向量$\overrightarrow{op}$的θ°坐标,记作$\overrightarrow{op}$(θ°)=(x,y);当θ=90°时,称(x,y)为$\overrightarrow{op}$的正交坐标.
如图,设ox,oy是平面内相交成θ°的两条数轴,$\overrightarrow{e_1}$,$\overrightarrow{e_2}$分别是与ox,oy正方向同向的单位向量,若向量$\overrightarrow{op}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则把有序实数对(x,y)叫做向量$\overrightarrow{op}$的θ°坐标,记作$\overrightarrow{op}$(θ°)=(x,y);当θ=90°时,称(x,y)为$\overrightarrow{op}$的正交坐标.