题目内容
18.某程序框图如图所示,若t=7,则输出的值为( )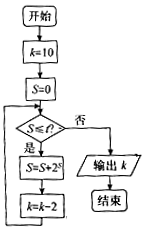
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
分析 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量k的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:当S=0时,满足继续循环的条件,则S=1,k=8;
当S=1时,满足继续循环的条件,则S=3,k=6;
当S=3时,满足继续循环的条件,则S=11,k=4;
不满足继续循环的条件,
故输出的k值为4,
故选:C.
点评 本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.

练习册系列答案
相关题目
8.一个扇形的圆心角为$\frac{2π}{3}$,半径为$\sqrt{3}$,则此扇形的面积为( )
| A. | π | B. | $\frac{5π}{4}$ | C. | $\frac{{\sqrt{3}π}}{3}$ | D. | $\frac{{2\sqrt{3}}}{9}{π^2}$ |
3.在某次测试后,一位老师从本班48同学中随机抽取6位同学,他们的语文、历史成绩如表:
(1)若规定语文成绩不低于90分为优秀,历史成绩不低于80分为优秀,以频率作概率,分别估计该班语文、历史成绩优秀的人数;
(2)用上表数据画出散点图易发现历史成绩y与语文成绩x具有较强的线性相关关系,求y与x的线性回归方程(系数精确到0.1).参考公式:回归直线方程是y=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$.
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 语文成绩x | 60 | 70 | 74 | 90 | 94 | 110 |
| 历史成绩y | 58 | 63 | 75 | 79 | 81 | 88 |
(2)用上表数据画出散点图易发现历史成绩y与语文成绩x具有较强的线性相关关系,求y与x的线性回归方程(系数精确到0.1).参考公式:回归直线方程是y=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$.
10.已知A(1,0),B(2,4),则$\overrightarrow{AB}$=( )
| A. | (-1,4) | B. | (1,-4) | C. | (-1,-4) | D. | (1,4) |
7.已知集合A={0,1,2},A∩B={0,2},则B集合可能是( )
| A. | {0,1} | B. | {1,2} | C. | {0,2,3} | D. | {0} |
8.下列命题中正确的是( )
| A. | 若α>β,则sinα>sinβ | |
| B. | 命题:“?x>1,x2>1”的否定是“?x≤1,x2≤1” | |
| C. | 已知函数f(x)=x3+ax2+bx+c,若f(x)在区间(-1,0)上单调递减,则a2+b2的取值范围为$[{\frac{9}{5},+∞})$ | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |
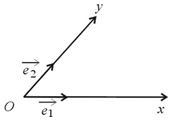 如图,设ox,oy是平面内相交成θ°的两条数轴,$\overrightarrow{e_1}$,$\overrightarrow{e_2}$分别是与ox,oy正方向同向的单位向量,若向量$\overrightarrow{op}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则把有序实数对(x,y)叫做向量$\overrightarrow{op}$的θ°坐标,记作$\overrightarrow{op}$(θ°)=(x,y);当θ=90°时,称(x,y)为$\overrightarrow{op}$的正交坐标.
如图,设ox,oy是平面内相交成θ°的两条数轴,$\overrightarrow{e_1}$,$\overrightarrow{e_2}$分别是与ox,oy正方向同向的单位向量,若向量$\overrightarrow{op}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则把有序实数对(x,y)叫做向量$\overrightarrow{op}$的θ°坐标,记作$\overrightarrow{op}$(θ°)=(x,y);当θ=90°时,称(x,y)为$\overrightarrow{op}$的正交坐标.