题目内容
20.已知一个算法:(1)m=a.
(2)如果b<m,则m=b,输出m;否则执行第3步.
(3)如果c<m,则m=c,输出m.
如果a=3,b=6,c=2,
那么执行这个算法的结果是( )
| A. | 3 | B. | 6 | C. | 2 | D. | m |
分析 逐步分析框图中的各框语句的功能,第二步条件结构是比较a,b的大小,并将a,b中的较小值保存在变量m中,第三步条件结构是比较a,c的大小,并将a,c中的较小值保存在变量m中,故变量m的值最终为a,b,c中的最小值,否则输出“无解”.由此不难推断执行这个算法的结果.
解答 解:逐步分析算法中的各语句的功能,
第一个条件结构是比较a,b的大小,
并将a,b中的较小值保存在变量m中,
第二个条件结构是比较a,c的大小,
并将a,c中的较小值保存在变量m中,
故变量m的值最终为a,b,c中的最小值.
由此程序的功能为求a,b,c三个数的最小数,∴m=2.
故选C.
点评 要判断程序的功能就要对程序的流程图(伪代码)逐步进行分析,分析出各变量值的变化情况,特别是输出变量值的变化情况,就不难得到正确的答案.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
8.一个扇形的圆心角为$\frac{2π}{3}$,半径为$\sqrt{3}$,则此扇形的面积为( )
| A. | π | B. | $\frac{5π}{4}$ | C. | $\frac{{\sqrt{3}π}}{3}$ | D. | $\frac{{2\sqrt{3}}}{9}{π^2}$ |
15.若?x>0,4a>x2-x3恒成立,则a的取值范围为( )
| A. | $({\frac{1}{27},+∞})$ | B. | $({\frac{4}{27},+∞})$ | C. | $[{\frac{1}{27},+∞})$ | D. | $[{\frac{4}{27},+∞})$ |
12.2016年春运期间为查醉酒驾驶,将甲、乙、丙三名交警安排到某商业中心附近的两个不同路口突击检查,每个路口至少一人,则甲、乙两名交警不在同一路口的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
10.已知A(1,0),B(2,4),则$\overrightarrow{AB}$=( )
| A. | (-1,4) | B. | (1,-4) | C. | (-1,-4) | D. | (1,4) |
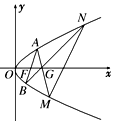 如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).
如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).