题目内容
4.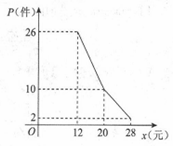 某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.(I)根据周销量图写出周销量P(件)与单价x(元)之间的函数关系式;
(Ⅱ)写出周利润y(元)与单价x(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
分析 (I)根据函数图象,求出解析式,即可写出周销量P(件)与单价x(元)之间的函数关系式;
(Ⅱ)分段求出最值,即可得出结论.
解答 解:(I)当x∈[12,20]时,P=k1x+b1,代入点(12,26),(20,10)得k1=-2,b1=50,∴P=-2x+50;
同理x∈(20,28]时,P=-x+30,
∴周销量P(件)与单价x(元)之间的函数关系式P=$\left\{\begin{array}{l}{-2x+50,12≤x≤20}\\{-x+30,20<x≤28}\end{array}\right.$;
(Ⅱ)y=P(x-10)-25=$\left\{\begin{array}{l}{(-2x+50)(x-10)-25,12≤x≤20}\\{(-x+30)(x-10),20<x≤28}\end{array}\right.$,
当x∈[12,20]时,y=$-2(x-\frac{35}{2})^{2}+\frac{175}{2}$,x=$\frac{35}{2}$时,ymax=$\frac{175}{2}$;
x∈(20,28]时,y=-(x-20)2+75,函数单调递减,∴y<75,
综上所述,x=$\frac{35}{2}$时,ymax=$\frac{175}{2}$.
点评 本题考查分段函数及运用,考查分段函数的最值,应考虑各段的最值,考查运算能力,属于中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
15.抛物线y=-$\frac{1}{8}{x}^{2}$的准线方程是( )
| A. | x=$\frac{1}{32}$ | B. | x=$\frac{1}{2}$ | C. | y=2 | D. | y=4 |
12.若tan(α-β)=$\frac{1}{2}$,tan(α+β)=$\frac{1}{3}$,则tan2β等于( )
| A. | $\frac{1}{7}$ | B. | $\frac{4}{3}$ | C. | -$\frac{1}{7}$ | D. | -$\frac{4}{3}$ |
19.设函数f(x)在(-∞,+∞)上有意义,对于给定的正数k,定义函数fk(x)=$\left\{\begin{array}{l}f(x),f(x)<k\\ k,f(x)≥k\end{array}\right.$,取k=3,f(x)=($\frac{k}{2}$)|x|,则fk(x)=$\frac{k}{2}$的零点有( )
| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | 不确定,随k的变化而变化 |
9.设函数f(x)在(-∞,+∞)上有意义,对于对定的正数k,定义函数fk(x)=$\left\{\begin{array}{l}{f(x),f(x)<k}\\{k,f(x)≥k}\end{array}\right.$取k=$\frac{1}{2}$,f(x)=($\frac{1}{2}$)|x|,则fk(x)=$\frac{k}{2}$的零点有( )
| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | 不确定,随k的变化而变化 |
20.设x,y∈R,下列不等式成立的是( )
| A. | 1+|x+y|+|xy|≥|x|+|y| | B. | 1+2|x+y|≥|x|+|y| | C. | 1+2|xy|≥|x|+|y| | D. | |x+y|+2|xy|≥|x|+|y| |
 如图,在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.
如图,在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.