题目内容
11.已知α∈(0,$\frac{π}{2}$),β∈(0,$\frac{π}{2}$),且满足$\sqrt{3}$cos2$\frac{α}{2}$+$\sqrt{2}$sin2$\frac{β}{2}$=$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$,sin(2017π-α)=$\sqrt{2}$cos($\frac{5}{2}$π-β),则α+β=$\frac{5}{12}$π.分析 由二倍角公式的变形、诱导公式化简已知的式子,利用平方关系、α和β的范围、特殊角的三角函数值求出α和β的值,可得α+β的值.
解答 解:∵$\sqrt{3}$cos2$\frac{α}{2}$+$\sqrt{2}$sin2$\frac{β}{2}$=$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$,
∴$\frac{\sqrt{3}}{2}$(1+cosα)+$\frac{\sqrt{2}}{2}$(1-cosβ)=$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$,
则$\frac{\sqrt{3}}{2}$cosα-$\frac{\sqrt{2}}{2}$cosβ=0,即$\sqrt{3}$cosα=$\sqrt{2}$cosβ,①
∵sin(2017π-α)=$\sqrt{2}$cos($\frac{5}{2}$π-β),
∴sin(π-α)=$\sqrt{2}$cos($\frac{1}{2}$π-β),
则sinα=$\sqrt{2}$sinβ,②
①2+②2得,3cos2α+sin2α=2,
则$co{s}^{2}α=\frac{1}{2}$,
由α∈(0,$\frac{π}{2}$)得cosα=$\frac{\sqrt{2}}{2}$,则α=$\frac{π}{4}$,
代入②可得,sinβ=$\frac{1}{2}$,
由β∈(0,$\frac{π}{2}$)得β=$\frac{π}{6}$,
∴α+β=$\frac{π}{4}$+$\frac{π}{6}$=$\frac{5π}{12}$,
故答案为:$\frac{5π}{12}$.
点评 本题考查二倍角公式的变形、诱导公式,三角函数值的符号,以及平方关系的应用,考查化简、变形能力.

| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | 不确定,随k的变化而变化 |
| A. | {-1} | B. | {2} | C. | {-1,2} | D. | {-1,0,1,2} |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
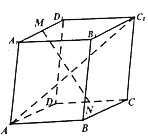 已知平行六面体ABCD-A1B1C1D1,设A1D1中点为M,CD的中点为N,若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1,则|AC1|=$\sqrt{6}$,若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=0.
已知平行六面体ABCD-A1B1C1D1,设A1D1中点为M,CD的中点为N,若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1,则|AC1|=$\sqrt{6}$,若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=0.