题目内容
15.函数f(x)=x3-3x2+x在点(1,f(1))处的切线方程为2x+y-1=0.分析 求导数,确定切线的斜率,利用点斜式,可得切线方程.
解答 解:求导数,可得f′(x)=3x2-6x+1,
∴f′(1)=-2,
∵f(1)=1-3+1=-1,
∴函数f(x)=x3-3x2+x在点(1,f(1))处的切线方程为:y+1=-2(x-1),即2x+y-1=0,
故答案为2x+y-1=0.
点评 本题考查导数的几何意义,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
6.若平面向量$\overrightarrow a$与$\overrightarrow{b}$的夹角60°,$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1$,|则$|{\overrightarrow a-2\overrightarrow b}|$=( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 1 | D. | 2 |
10.执行如图所示的程序框图,若输出S的值为0.99,则判断框内可填入的条件是( )
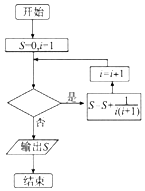

| A. | i<100 | B. | i≤100 | C. | i<99 | D. | i≤98 |
7.已知复数$\frac{a+ai}{2-ai}$为纯虚数(其中i为虚数单位),则实数a的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
4.在长方体ABCD-A1B1C1D1中,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$,则$\overrightarrow{A{C}_{1}}$=( )
| A. | $\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$ | B. | $\overrightarrow{a}$-$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$ | D. | -$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$ |
2.等比数列{an}中,a2=4,a6和a2的等比中项等于±6,则a6=( )
| A. | 9 | B. | -9 | C. | ±8 | D. | 8 |