题目内容
3．4人站成一排，其中甲乙相邻则共有12种不同的排法．分析 相邻问题运用捆绑法，甲乙捆绑，再与其它2人，全排即可．
解答 解：相邻问题运用捆绑法，甲乙捆绑，再与其它2人，全排，
故甲、乙二人相邻的不同排法共A22•A33=12种．
故答案为：12．
点评 本题主要考查了相邻问题，采用捆绑法关键，属于基础题．
练习册系列答案
相关题目
13．已知全集U={1，2，3，4，5，6，7，8}，集合A={2，3，5，6}，集合B={1，3，4，6}，则A∪（∁UB）=（ ）
| A． | {2，5} | B． | {2，5，7，8} | C． | {2，3，5，6，7，8} | D． | {1，2，3，4，5，6} |
12．已知平面区域Ω={（x，y）|x＞0，y＞0，x+y＜2}，A={（x，y）|x＜1，y＜1，x+y＞1}，若在区间Ω内随机投一点P，则点P落入区域A的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
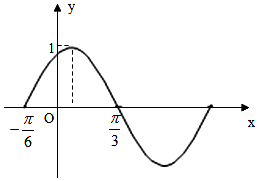已知函数f（x）=Asin（ωx+ϕ）（其中A＞0，|ϕ|＜$\frac{π}{2}$，ω＞0）的图象如图所示，