题目内容
20.已知函数f(x)=$\frac{1}{2}$x2+ax-2lnx(a∈R).(1)若a=1,求函数f(x)的单调区间和极值;
(2)若函数f(x)在区间(0,2]上单调递减,求实数a的取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间和极值即可;
(2)问题转化为$a≤\frac{2}{x}-x$在区间(0,2]上恒成立,设$g(x)=\frac{2}{x}-x$,根据函数的单调性求出a的范围即可.
解答 解:(1)$f(x)=\frac{1}{2}{x^2}+ax-2lnx$.
当a=1时,$f(x)=\frac{1}{2}{x^2}+x-2lnx$,定义域为(0,+∞).
其导函数为$f'(x)=x+1-\frac{2}{x}=\frac{{{x^2}+x-2}}{x}=\frac{(x+2)(x-1)}{x}$
令f'(x)>0可得:x>1;
令f'(x)<0可得:0<x<1.
故函数f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1),
f(x)的极小值为$f(1)=\frac{3}{2}$,无极大值.
(2)f(x)的导函数为$f'(x)=x+a-\frac{2}{x}=\frac{{{x^2}+ax-2}}{x}$,
由函数f(x)在区间(0,2]上为减函数可得:
f'(x)≤0即x2+ax-2≤0在区间(0,2]上恒成立,
即$a≤\frac{2}{x}-x$在区间(0,2]上恒成立,
设$g(x)=\frac{2}{x}-x$,可知y=g(x)在(0,2]上单调递减,
所以a≤gmin(x)=g(2)=-1.
故所求实数a的取值范围为(-∞,-1].
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及函数恒成立问题,是一道中档题.

练习册系列答案
相关题目
10.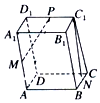 如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )
如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )
 如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )
如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )| A. | $\frac{3}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{3}{2}\overrightarrow c$ | B. | $\overrightarrow a+\frac{1}{2}\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | D. | $\frac{3}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$ |
12.已知平面区域Ω={(x,y)|x>0,y>0,x+y<2},A={(x,y)|x<1,y<1,x+y>1},若在区间Ω内随机投一点P,则点P落入区域A的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
7.设x,y满足约束条件$\left\{\begin{array}{l}{2x-y+2≥0}\\{8x-y-4≤0}\\{x≥0,y≥0}\end{array}\right.$,若目标函数z=abx+y(a>0,b>0)的最大值为18,则2a+b的最小值为( )
| A. | 4 | B. | 2$\sqrt{7}$ | C. | 4$\sqrt{7}$ | D. | 4$\sqrt{14}$ |
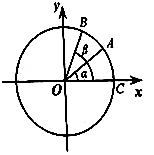 如图,在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点A($\frac{4}{5}$,$\frac{3}{5}$),B($\frac{5}{13}$,$\frac{12}{13}$).
如图,在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点A($\frac{4}{5}$,$\frac{3}{5}$),B($\frac{5}{13}$,$\frac{12}{13}$).