题目内容
①若函数y=2x的定义域是{x|x≤0},则它的值域是{y|y≤1};
②若函数y=
的定义域是{x|x>2},则它的值域是{y|y≤
};
③若函数y=x2的值域是{y|0≤y≤4},则它的定义域是{x|-2≤x≤2};
④若函数y=log2x的值域是{y|y≤3},则它的定义域是{x|x≤8};
你认为其中不正确的命题的序号是 .
②若函数y=
| 1 |
| x |
| 1 |
| 2 |
③若函数y=x2的值域是{y|0≤y≤4},则它的定义域是{x|-2≤x≤2};
④若函数y=log2x的值域是{y|y≤3},则它的定义域是{x|x≤8};
你认为其中不正确的命题的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:直接利用基本初等函数的单调性由定义域求得函数值域判断命题①②;
由函数的概念,结合函数的自变量和函数值的对应关系判断命题③④.
由函数的概念,结合函数的自变量和函数值的对应关系判断命题③④.
解答:
解:对于①,∵函数y=2x是增函数且定义域是{x|x≤0},
∴它的值域是{y|0<y≤1},命题①错误;
对于②,函数y=
在{x|x>2}上为减函数,
∴它的值域是{y|0<y<
},命题②错误;
对于③,当x∈[0,2]时,函数y=x2的值域是{y|0≤y≤4},
∴命题③错误;
对于④,∵函数y=log2x是(0,+∞)上的增函数,若函数y=log2x的值域是{y|y≤3},
则其定义域为{x|0<x≤8}.
∴命题④错误.
∴其中不正确的命题的序号是①②③④.
故答案为:①②③④.
∴它的值域是{y|0<y≤1},命题①错误;
对于②,函数y=
| 1 |
| x |
∴它的值域是{y|0<y<
| 1 |
| 2 |
对于③,当x∈[0,2]时,函数y=x2的值域是{y|0≤y≤4},
∴命题③错误;
对于④,∵函数y=log2x是(0,+∞)上的增函数,若函数y=log2x的值域是{y|y≤3},
则其定义域为{x|0<x≤8}.
∴命题④错误.
∴其中不正确的命题的序号是①②③④.
故答案为:①②③④.
点评:本题考查了命题的真假判断与应用,考查了由函数的单调性求解函数的值域,是中档题.

练习册系列答案
相关题目
在盒子中装有2个白球和2个红球,每次从中随机取出一个球,第三次恰好将白球取完的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=x+
,则函数y=f(x)的大致图象为( )
| ln|x| |
| x |
A、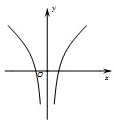 |
B、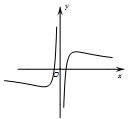 |
C、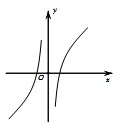 |
D、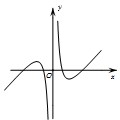 |