题目内容
直线l的倾斜角α满足3sinα=4cosα,且它在x轴上的截距为2,则直线l的方程是 .
考点:直线的截距式方程,直线的倾斜角
专题:直线与圆
分析:根据条件先求出直线的斜率,然后利用点斜式方程即可求直线方程.
解答:
解:∵直线l的倾斜角α满足3sinα=4cosα,
∴tanα=
,即直线的斜率k=tanα=
,
∵在x轴上的截距为2,
∴直线过点(2,0),
则直线的方程为y-0=
(x-2),
即4x-3y-8=0,
故答案为:4x-3y-8=0.
∴tanα=
| 4 |
| 3 |
| 4 |
| 3 |
∵在x轴上的截距为2,
∴直线过点(2,0),
则直线的方程为y-0=
| 4 |
| 3 |
即4x-3y-8=0,
故答案为:4x-3y-8=0.
点评:本题主要考查直线方程的求法,根据条件求出直线斜率和定点坐标是解决本题的关键,比较基础.

练习册系列答案
相关题目
给出下列语句:
①二次函数是偶函数吗?
②2>2;
③sin
=1;
④x2-4x+4=0.
其中是命题的有( )
①二次函数是偶函数吗?
②2>2;
③sin
| π |
| 2 |
④x2-4x+4=0.
其中是命题的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
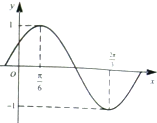 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<