题目内容
若命题“?x0∈R,2x02-3mx0+9<0”为假命题,则实数m的取值范围是 .
考点:特称命题,命题的真假判断与应用
专题:简易逻辑
分析:由于命题“?x0∈R,2x02-3mx0+9<0”为假命题,可得其非命题:“?x∈R,2x2-3mx+9≥0”为真命题.于是△≤0解出即可.
解答:
解:∵命题“?x0∈R,2x02-3mx0+9<0”为假命题,
∴其非命题:“?x∈R,2x2-3mx+9≥0”为真命题.
∴△=(-3m)2-72≤0,
∴m2≤8,解得-2
≤m≤2
.
∴实数m的取值范围是[-2
,2
].
故答案为:[-2
,2
].
∴其非命题:“?x∈R,2x2-3mx+9≥0”为真命题.
∴△=(-3m)2-72≤0,
∴m2≤8,解得-2
| 2 |
| 2 |
∴实数m的取值范围是[-2
| 2 |
| 2 |
故答案为:[-2
| 2 |
| 2 |
点评:本题考查了命题与其非命题的真假关系、一元二次不等式恒成立问题与判别式之间的关系,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
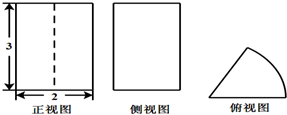 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的侧面积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的侧面积为( )A、12+
| ||
B、6+
| ||
| C、12+2π | ||
| D、6+4π |
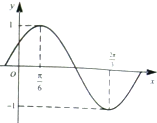 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<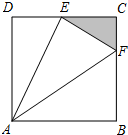 如图,ABCD是边长为1百米的正方形区域,现规划建造一块景观带△ECF,其中动点E、F分别在CD、BC上,且△ECF的周长为常数a(单位:百米).
如图,ABCD是边长为1百米的正方形区域,现规划建造一块景观带△ECF,其中动点E、F分别在CD、BC上,且△ECF的周长为常数a(单位:百米). 如图,设F(-c,0)是椭圆
如图,设F(-c,0)是椭圆