题目内容
11.已知函数g(x)=lnx-ax2+(2-a)x,a∈R.(1)求g(x)的单调区间;
(2)若函数f(x)=g(x)+(a+1)x2-2x,x1,x2(x1<x2)是函数f(x)的两个零点,f′(x)是函数f(x)的导函数,证明:f′($\frac{{x}_{1}+{x}_{2}}{2}$)<0.
分析 (1)先求函数的定义域,求函数的导数,在定义域内讨论函数的单调性;
(2)求出a=$\frac{l{nx}_{1}-l{nx}_{2}}{{{x}_{1}-x}_{2}}$+x1+x2,问题转化为证明$\frac{2{(x}_{1}{-x}_{2})}{{{x}_{1}+x}_{2}}$>lnx1-lnx2,即证明$\frac{2(\frac{{x}_{1}}{{x}_{2}}-1)}{\frac{{x}_{1}}{{x}_{2}}+1}$>ln$\frac{{x}_{1}}{{x}_{2}}$(*),令$\frac{{x}_{1}}{{x}_{2}}$=t∈(0,1),则h(t)=(1+t)lnt-2t+2,根据函数的单调性证明即可.
解答 解:(1)函数f(x)=lnx-ax2+(2-a)x的定义域为(0,+∞),
f′(x)=$\frac{1}{x}$-2ax+(2-a)=-$\frac{(ax-1)(2x+1)}{x}$,
①当a≤0时,f′(x)>0,x∈(0,+∞),
则f(x)在(0,+∞)上单调递增;
②当a>0时,x∈(0,$\frac{1}{a}$)时,f′(x)>0,
x∈($\frac{1}{a}$,+∞)时,f′(x)<0,
则f(x)在(0,$\frac{1}{a}$)上单调递增,在($\frac{1}{a}$,+∞)上单调递减;
(2)由x1,x2(x1<x2)是函数f(x)的两个零点,
得f(x1)=lnx1+${{x}_{1}}^{2}$-ax1=0,f(x2)=lnx2+${{x}_{2}}^{2}$-ax2=0,
两式相减得a=$\frac{l{nx}_{1}-l{nx}_{2}}{{{x}_{1}-x}_{2}}$+x1+x2,
∵f′(x)=$\frac{1}{x}$+2x-a,
∴f′($\frac{{x}_{1}{+x}_{2}}{2}$)=$\frac{2}{{{x}_{1}+x}_{2}}$-$\frac{l{nx}_{1}-l{nx}_{2}}{{{x}_{1}-x}_{2}}$,
故要证明f′($\frac{{x}_{1}+{x}_{2}}{2}$)<0,
只需证明$\frac{2}{{{x}_{1}+x}_{2}}$-$\frac{l{nx}_{1}-l{nx}_{2}}{{{x}_{1}-x}_{2}}$<0,(0<x1<x2),
即证明$\frac{2{(x}_{1}{-x}_{2})}{{{x}_{1}+x}_{2}}$>lnx1-lnx2,即证明$\frac{2(\frac{{x}_{1}}{{x}_{2}}-1)}{\frac{{x}_{1}}{{x}_{2}}+1}$>ln$\frac{{x}_{1}}{{x}_{2}}$(*),
令$\frac{{x}_{1}}{{x}_{2}}$=t∈(0,1),则h(t)=(1+t)lnt-2t+2,
则h′(t)=lnt+$\frac{1}{t}$-1,h″(x)=$\frac{1}{t}$-$\frac{1}{{t}^{2}}$<0,
故h′(t)在(0,1)递减,h′(t)>h′(1)=0,
故h(t)在(0,1)递增,h(t)<h(1)=0,
故(*)成立,即f′($\frac{{x}_{1}+{x}_{2}}{2}$)<0.
点评 本题考查了函数的单调性、最值问题,考查不等式的证明以及转化思想,是一道综合题.

| A. | $\sqrt{5}$ | B. | 5 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{17}$ |
| A. | 偶函数且它的图象关于点(π,0)对称 | |
| B. | 偶函数且它的图象关于点$(\frac{3π}{2},0)$对称 | |
| C. | 奇函数且它的图象关于点(π,0)对称 | |
| D. | 奇函数且它的图象关于点$(\frac{3π}{2},0)$对称 |
| A. | x+y-2=0 | B. | y-1=0 | C. | x+3y-4=0 | D. | x-y=0 |
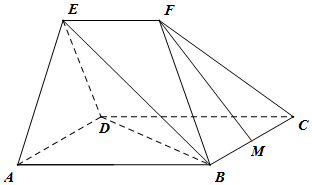 如图,在几何体ABCDEF中,平面ADE⊥平面ABCD,四边形ABCD为菱形,且∠DAB=60°,EA=ED=AB=2EF,EF∥AB,M为BC中点.
如图,在几何体ABCDEF中,平面ADE⊥平面ABCD,四边形ABCD为菱形,且∠DAB=60°,EA=ED=AB=2EF,EF∥AB,M为BC中点.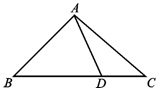 在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{{\sqrt{2}c-a}}{cosA}=\frac{b}{cosB}$,D是BC边上的一点.
在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{{\sqrt{2}c-a}}{cosA}=\frac{b}{cosB}$,D是BC边上的一点.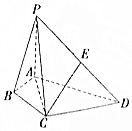 如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.
如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.