题目内容
2.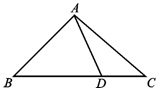 在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{{\sqrt{2}c-a}}{cosA}=\frac{b}{cosB}$,D是BC边上的一点.
在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{{\sqrt{2}c-a}}{cosA}=\frac{b}{cosB}$,D是BC边上的一点.(Ⅰ) 求角B的大小;
(Ⅱ) 若AC=7,AD=5,DC=3,求AB的长.
分析 (Ⅰ)根据三角形内角和定理和正弦定理化简可得角B的大小;
(Ⅱ)根据余弦定理,求出∠ADC,在利用正弦定理即可求AB的长.
解答 解:(Ⅰ) 由$\frac{{\sqrt{2}c-a}}{cosA}=\frac{b}{cosB}$,
得$\sqrt{2}ccosB-acosB=bcosA$,即$\sqrt{2}ccosB=acosB+bcosA$,
根据正弦定理,$\sqrt{2}sinCcosB=sinAcosB+sinBcosA=sin(A+B)=sinC$.
∴$cosB=\frac{{\sqrt{2}}}{2}$,
又0°<B<180°,
∴B=45°.
(Ⅱ) 在△ADC中,AC=7,AD=5,DC=3,
由余弦定理得$cos∠ADC=\frac{{A{D^2}+D{C^2}-A{C^2}}}{2AD•DC}$=$\frac{{{5^2}+{3^2}-{7^2}}}{2×5×3}=-\frac{1}{2}$,
∴∠ADC=120°,∠ADB=60°,
在△ABD中,AD=5,∠B=45°,∠ADB=60°,
由正弦定理,得$\frac{AB}{sin∠ADB}=\frac{AD}{sinB}$,
故得AB=$\frac{AD•sin∠ADB}{sinB}=\frac{5sin60°}{sin45°}=\frac{{5×\frac{{\sqrt{3}}}{2}}}{{\frac{{\sqrt{2}}}{2}}}=\frac{{5\sqrt{6}}}{2}$.
点评 本题考查三角形的正余弦定理和内角和定理的运用,考查运算能力,属于基础题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
5.已知函数f(x)=2cos(ωx+$\frac{3}{2}$π)(ω>0)的最小正周期为2π,则函数f(x)图象的一条对称轴方程为( )
| A. | x=$\frac{π}{4}$ | B. | x=$\frac{π}{2}$ | C. | x=$\frac{3}{4}$π | D. | x=π |
7.已知等轴双曲线C的一个焦点是F1(-6,0),点M是等轴双曲线的渐近线上的一个动点,点P是圆(x+6)2+y2=1上的任意一点,则|PM|的最小值是( )
| A. | 3$\sqrt{2}$-1 | B. | 2$\sqrt{3}$-1 | C. | 3$\sqrt{3}$+1 | D. | 2$\sqrt{3}$+2 |
14.设等差数列{an}的前n项和为Sn,Sm-1=13,Sm=0,Sm+1=-15.其中m∈N*且m≥2,则数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和的最大值为( )
| A. | $\frac{24}{143}$ | B. | $\frac{1}{143}$ | C. | $\frac{24}{13}$ | D. | $\frac{6}{13}$ |
12.已知函数f(x)=x(a-$\frac{1}{e^x}$),曲线y=f(x)上存在两个不同点,使得曲线在这两点处的切线都与y轴垂直,则实数a的取值范围是( )
| A. | (-e2,+∞) | B. | (-e2,0) | C. | (-$\frac{1}{e^2}$,+∞) | D. | (-$\frac{1}{e^2}$,0) |