题目内容

20．过点P（1，1）的直线，将圆形区域{x，y）|（x-2）2+y2≤4}分成两部分，使得这两部分的面积之差最大，则该直线的方程为（　　）
A．x+y-2=0B．y-1=0C．x+3y-4=0D．x-y=0

分析 要使面积之差最大，必须使过点P的弦最小，该直线与直线CP垂直，求得直线的斜率，再由点斜式可求得直线方程．

解答 解：圆形区域的圆心坐标为（2，0）．
要使面积之差最大，必须使过点P的弦最小，∴该直线与直线CP垂直．
又kCP=-1，所以直线的斜率为1，由点斜式可求得直线方程为y-1=x-1，即 x-y=0，
故选：D．

点评 本题主要考查直线和圆的位置关系，用点斜式求直线的方程，属于基础题．

练习册系列答案
相关题目
3．已知直线$l：\left\{\begin{array}{l}x=2+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.（t$为参数），曲线$C：\left\{\begin{array}{l}x=cosθ\\ y=sinθ\end{array}\right.（θ$为参数）．
（1）使判断l与C的位置关系；
（2）若把曲线C1上个点的横坐标压缩为原来的$\frac{1}{2}$倍，纵坐标压缩为原来的$\frac{{\sqrt{3}}}{2}$倍，得到曲线C2，设点P是曲线C2上一个动点，求它到直线l的距离的最小值．
11．已知函数g（x）=lnx-ax2+（2-a）x，a∈R．
（1）求g（x）的单调区间；
（2）若函数f（x）=g（x）+（a+1）x2-2x，x1，x2（x1＜x2）是函数f（x）的两个零点，f′（x）是函数f（x）的导函数，证明：f′（$\frac{{x}_{1}+{x}_{2}}{2}$）＜0．
8．在△ABC中，角A、B、C所对的边分别为a，b，c，满足（2a-c）cosB=bcosC．
（1）求B的大小；
（2）如图，AB=AC，在直线AC的右侧取点D，使得AD=2CD=4．当角D为何值时，四边形ABCD面积最大．
15．已知$f（x）=sinxcosx-{cos^2}（x+\frac{π}{4}）$x∈[-π，0]，则f（x）的单调减区间为$[-\frac{3π}{4}，0]$．
5．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的短轴一个端点到右焦点F的距离为2，且过点$（{-1，-\frac{{\sqrt{3}}}{2}}）$．
（1）求椭圆C的方程；
（2）设M，N为椭圆C上不同的两点，A，B分别为椭圆C上的左右顶点，直线MN既不平行与坐标轴，也不过椭圆C的右焦点F，若∠AFM=∠BFN，求证：直线MN过定点．
12．已知函数f（x）=x（a-$\frac{1}{e^x}$），曲线y=f（x）上存在两个不同点，使得曲线在这两点处的切线都与y轴垂直，则实数a的取值范围是（　　）
A．（-e2，+∞）B．（-e2，0）C．（-$\frac{1}{e^2}$，+∞）D．（-$\frac{1}{e^2}$，0）
9．某程序框图如图所示，则该程序运行后输出的值是（　　）
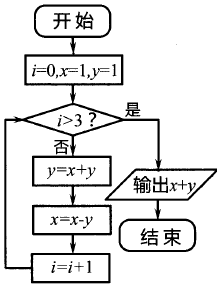
A．0B．-1C．-2D．-8
10．已知椭圆C：$\frac{{x{\;}^2}}{4}+\frac{y^2}{3}=1$，点P（4，0），过右焦点F作与y轴不垂直的直线l交椭圆C于A，B两点．
（Ⅰ）求椭圆C的离心率；
（Ⅱ）求证：以坐标原点O为圆心与PA相切的圆，必与直线PB相切．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网