题目内容
6.已知实数4,m,9构成一个等比数列,则圆锥曲线$\frac{{x}^{2}}{m}$+y2=1的焦距为2$\sqrt{5}$或2$\sqrt{7}$.分析 根据题意,由等比数列的性质可得m2=4×9=36,解可得m的值,分2种情况讨论:当m=6时,圆锥曲线的方程为$\frac{{x}^{2}}{6}$+y2=1,为椭圆,当m=-6时,圆锥曲线的方程为y2-$\frac{{x}^{2}}{6}$=1,为双曲线,由椭圆和双曲线的几何性质分析可得c的值,进而由焦距的定义可得答案.
解答 解:根据题意,实数4,m,9构成一个等比数列,则有m2=4×9=36,
则m=±6,
当m=6时,圆锥曲线的方程为$\frac{{x}^{2}}{6}$+y2=1,为椭圆,
其中a=$\sqrt{6}$,b=1,则c=$\sqrt{6-1}$=$\sqrt{5}$,
则其焦距2c=2$\sqrt{5}$,
当m=-6时,圆锥曲线的方程为y2-$\frac{{x}^{2}}{6}$=1,为双曲线,
其中a=1,b=$\sqrt{6}$,则c=$\sqrt{6+1}$=$\sqrt{7}$,
则其焦距2c=2$\sqrt{7}$,
综合可得:圆锥曲线$\frac{{x}^{2}}{m}$+y2=1的焦距为2$\sqrt{5}$或2$\sqrt{7}$;
故答案为:2$\sqrt{5}$或2$\sqrt{7}$.
点评 本题考查椭圆、双曲线的几何性质,关键是由等比数列的性质求出m的值,确定圆锥曲线的方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.设等差数列{an}的前n项和为Sn,Sm-1=13,Sm=0,Sm+1=-15.其中m∈N*且m≥2,则数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和的最大值为( )
| A. | $\frac{24}{143}$ | B. | $\frac{1}{143}$ | C. | $\frac{24}{13}$ | D. | $\frac{6}{13}$ |
1.已知平面下列$\overrightarrow{a}$=(-2,3),$\overrightarrow{b}$=(1,2),向量λ$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{b}$垂直,则实数λ的值为( )
| A. | $\frac{4}{13}$ | B. | -$\frac{4}{13}$ | C. | $\frac{5}{4}$ | D. | -$\frac{5}{4}$ |
16.已知集合A={x|x2-x+4>x+12},B={x|2x-1<8},则A∩(∁RB)=( )
| A. | {x|x≥4} | B. | {x|x>4} | C. | {x|x≥-2} | D. | {x|x<-2或x≥4} |
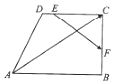 如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=3,BC=DC=2,若E,F分别是线段DC和BC上的动点,则$\overrightarrow{AC}•\overrightarrow{EF}$的取值范围是[-4,6].
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=3,BC=DC=2,若E,F分别是线段DC和BC上的动点,则$\overrightarrow{AC}•\overrightarrow{EF}$的取值范围是[-4,6].