题目内容
某花木公司为了调查某种树苗的生长情况,抽取了一个容量为100的样本,测得树苗的高度(cm)数据的分组及相应频数如下:
[107,109)3株;[109,111)9株;[111,113)13株;[113,115)16株;[115,117)26株;
[117,119)20株;[119,121)7株;[121,123)4株;[123,125)2株.
(1)列出频率分布表.
(2)画出频率分布直方图.
(3)据上述图表,估计数据落在[109,121)范围内的可能性是百分之几?
(4)求出数据的中位数.
[107,109)3株;[109,111)9株;[111,113)13株;[113,115)16株;[115,117)26株;
[117,119)20株;[119,121)7株;[121,123)4株;[123,125)2株.
(1)列出频率分布表.
(2)画出频率分布直方图.
(3)据上述图表,估计数据落在[109,121)范围内的可能性是百分之几?
(4)求出数据的中位数.
考点:众数、中位数、平均数,频率分布直方图
专题:概率与统计
分析:(1)计算出各组的频率及累积频率,列出分布表;
(2)根据(1)中样本的频率分布表(含累积频率),画出频率分布直方图;
(3)根据(2)中的频率分布直方图,估计数据落在[109,121)范围内的可能性是百分之几.
(4)把数据按从小到大排列,按中位数的定义求解.
(2)根据(1)中样本的频率分布表(含累积频率),画出频率分布直方图;
(3)根据(2)中的频率分布直方图,估计数据落在[109,121)范围内的可能性是百分之几.
(4)把数据按从小到大排列,按中位数的定义求解.
解答:
解:(1)画出频率分布表,图形如下:
(2)画出频率分布直方图:
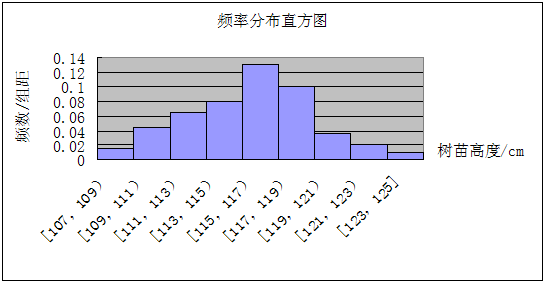
(3)由上述图表可知数据落在[109,121)范围内的频率为:
0.94-0.03=0.91,
即数据落[109,121)范围内的可能性是91%.
(4)∵[107,109)3株;[109,111)9株;[111,113)13株;[113,115)16株;[115,117)26株;
[117,119)20株;[119,121)7株;[121,123)4株;[123,125)2株.
∴中位数=
=116.
| 分组 | 频数 | 频率 | 累积频率 |
| [107,109) | 3 | 0.03 | 0.03 |
| [109,111) | 9 | 0.09 | 0.12 |
| [111,113) | 13 | 0.13 | 0.25 |
| [113,115) | 16 | 0.16 | 0.41 |
| [115,117) | 26 | 0.26 | 0.67 |
| [117,119) | 20 | 0.20 | 0.87 |
| [119,121) | 7 | 0.07 | 0.94 |
| [121,123) | 4 | 0.04 | 0.98 |
| [123,125] | 2 | 0.02 | 1.00 |
| 合计 | 100 | 1.00 |

(3)由上述图表可知数据落在[109,121)范围内的频率为:
0.94-0.03=0.91,
即数据落[109,121)范围内的可能性是91%.
(4)∵[107,109)3株;[109,111)9株;[111,113)13株;[113,115)16株;[115,117)26株;
[117,119)20株;[119,121)7株;[121,123)4株;[123,125)2株.
∴中位数=
| 115+117 |
| 2 |
点评:本题主要考查频率分布直方图和表,还考查同学们通过已知数据作出频数直方图、表的能力.

练习册系列答案
相关题目
下列命题中正确的是( )
A、“cosα=
| ||||
| B、函数y=f(x)在区间(a,b)内有零点,则f(a)•f(b)<0 | ||||
| C、数列{an}是等比数列的充要条件是an+12=anan+2(n∈N*) | ||||
| D、命题“?x∈R,2x>0”的否定是“?x∈R,2x≤0”. |
下列函数在定义域内为奇函数,且有最小值的是( )
A、y=x+
| ||
| B、y=xsinx | ||
| C、y=x(|x|-1) | ||
D、y=cos(x-
|
 春暖花开季节,某校举行了踢毽子比赛,将所得数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5.
春暖花开季节,某校举行了踢毽子比赛,将所得数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5. 如图,射线OA,OB与x轴正半轴的夹角分别为45°和30°,过点P(1,0)的直线l分别交OA,OB于点A,B.
如图,射线OA,OB与x轴正半轴的夹角分别为45°和30°,过点P(1,0)的直线l分别交OA,OB于点A,B.