题目内容
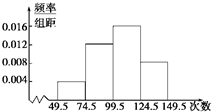 春暖花开季节,某校举行了踢毽子比赛,将所得数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5.
春暖花开季节,某校举行了踢毽子比赛,将所得数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5.(1)求第四小组的频率;
(2)参加这次比赛的学生人数是多少?
(3)在这次比赛中,学生踢毽子的中位数落在第几小组内?
考点:众数、中位数、平均数,频率分布直方图
专题:概率与统计
分析:(1)1减其余各小组的频率之和,得到第四小组的频率
(2)设参加这次测试的学生人数为
.
(3)由已知条件分别求出第一、第二、第三、第四小组的频数,由此能求出学生踢毽子次数的中位数落在第几小组内.
(2)设参加这次测试的学生人数为
| 第一小组频数 |
| 第一小组频率 |
(3)由已知条件分别求出第一、第二、第三、第四小组的频数,由此能求出学生踢毽子次数的中位数落在第几小组内.
解答:
解:(1)第四小组的频率=1-(0.1+0.3+0.4)=0.2.(4分)
(2)设参加这次测试的学生人数是n,则有
n=
=5÷0.1=50(人).(8分)
(3)∵0.1×50=5,0.3×50=15,
0.4×50=20,0.2×50=10,
即第一、第二、第三、第四小组的频数分别为5、15、20、10,
所以学生踢毽子次数的中位数落在第三小组内.(12分)
(2)设参加这次测试的学生人数是n,则有
n=
| 第一小组频数 |
| 第一小组频率 |
(3)∵0.1×50=5,0.3×50=15,
0.4×50=20,0.2×50=10,
即第一、第二、第三、第四小组的频数分别为5、15、20、10,
所以学生踢毽子次数的中位数落在第三小组内.(12分)
点评:本题考查频率分布直方图的应用,是基础题,解题时要认真审题,要注意识图能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,三个正方形并排放置,则∠BAE+∠CAD=( )


A、
| ||
B、
| ||
| C、75° | ||
| D、以上都不对 |