题目内容
1.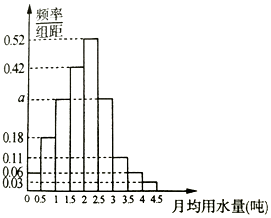 我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超过x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超过x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(Ⅰ)求直方图中a的值;
(Ⅱ)若将频率视为概率,从该城市居民中随机抽取3人,记这3人中月均用水量不低于3吨的人数为X,求X的分布列与数学期望.
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值(精确到0.01),并说明理由.
分析 (Ⅰ)根据频率和为1,列出方程求得a的值;
(Ⅱ)计算月均用水量不低于3吨的频率值,由抽取的人数X的可能取值为0,1,2,3;
计算对应的概率值,写出X的分布列,计算数学期望值;
(Ⅲ)计算月均用水量小于2.5吨和小于3吨的百分比,
求出有85%的居民月用水量不超过的标准值.
解答 解:(Ⅰ)根据频率和为1,得
(0.06+0.18+2a+0.42+0.52+0.11+0.06+0.03)×0.5=1,
解得a=0.30;
(Ⅱ)月均用水量不低于3吨的频率为
(0.11+0.06+0.03)×0.5=0.1,
则p=0.1,抽取的人数为X,
则X的可能取值为0,1,2,3;
∴P(X=0)=${C}_{3}^{0}$•0.93=0.729,
P(X=1)=${C}_{3}^{1}$•0.1•0.92=0.243,
P(X=2)=${C}_{3}^{2}$•0.12•0.9=0.027,
P(X=3)=${C}_{3}^{3}$•0.13=0.001;
∴X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | 0.729 | 0.243 | 0.027 | 0.001 |
(Ⅲ)由图可知,月均用水量小于2.5吨的居民人数所占的百分比为
0.5×(0.06+0.18+0.3+0.42+0.52)=0.73,
即73%的居民月均用水量小于2.5吨;
同理,88%的居民月均用水量小于3吨;
故2.5<x<3,
假设月均用水量平均分布,则
x=2.5+0.5×$\frac{(0.85-0.73)÷0.5}{0.3}$=2.9(吨),
即85%的居民每月用水量不超过标准为2.9吨.
点评 本题考查了频率分布直方图的应用问题,也考查了离散型随机变量的分布列与数学期望的计算问题,是中档题.

练习册系列答案
相关题目
9.若sinα=$\frac{5}{13}$,且α为第二象限角,则tanα的值等于( )
| A. | $\frac{12}{5}$ | B. | -$\frac{12}{5}$ | C. | $\frac{5}{12}$ | D. | -$\frac{5}{12}$ |
6.z=3-4i,则复数z-|z|+(1-i)在复平面内的对应点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,O为坐标原点,点F为抛物线C1:x2=2py(p>0)的焦点,且抛物线C1上点M处的切线与圆C2:x2+y2=1相切于点Q.
如图,O为坐标原点,点F为抛物线C1:x2=2py(p>0)的焦点,且抛物线C1上点M处的切线与圆C2:x2+y2=1相切于点Q.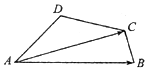 在四边形ABCD中,∠ADC=∠BCD=120°,AD=DC=2CB=1,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=3.
在四边形ABCD中,∠ADC=∠BCD=120°,AD=DC=2CB=1,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=3.