题目内容
16．已知复数z满足：|z|=1+3i-z，求$\frac{3+4i}{Z}$的值．分析 设z=a+bi，（a，b∈R），代入|z|=1+3i-z，利用复数相等的条件列式求得a，b的值，再由复数代数形式的乘除运算化简得答案．
解答 解：设z=a+bi，（a，b∈R），
而|z|=1+3i-z，即$\sqrt{{a}^{2}+{b}^{2}}-1-3i+a+bi=0$，
则$\left\{\begin{array}{l}{\sqrt{{a}^{2}+{b}^{2}}+a-1=0}\\{b-3=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=-4}\\{b=3}\end{array}\right.$，∴z=-4+3i．
∴$\frac{3+4i}{z}=\frac{3+4i}{-4+3i}=\frac{（3+4i）（-4-3i）}{（-4+3i）（-4-3i）}$=$\frac{-25i}{25}=-i$．
点评 本题考查复数代数形式的乘除运算，考查了复数相等的条件，是基础题．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
13．设曲线f（x）=Asin（x+θ）（A＞0）的一条对称轴为$x=\frac{π}{5}$，则曲线$y=f（\frac{π}{10}-x）$的一个对称点为（ ）
| A． | $（\frac{π}{5}，0）$ | B． | $（\frac{2π}{5}，0）$ | C． | $（\frac{3π}{5}，0）$ | D． | $（\frac{4π}{5}，0）$ |
4．已知向量$\overrightarrow{a}$=（$\sqrt{3}$，-1），向量$\overrightarrow{b}$=（1+tcos$\frac{π}{5}$，tsin$\frac{π}{5}$）（t＞0），则向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角可能是（ ）
| A． | $\frac{π}{9}$ | B． | $\frac{5π}{18}$ | C． | $\frac{7π}{18}$ | D． | $\frac{11π}{18}$ |
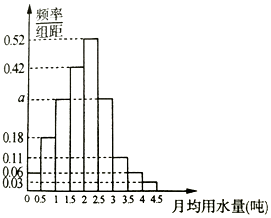我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超过x的部分按议价收费．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），…，[4，4.5）分成9组，制成了如图所示的频率分布直方图．
8．椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{169}$=1的焦点坐标为（ ）
| A． | （5，0），（-5，0） | B． | （0，5），（0，-5） | C． | （0，12），（0，-12） | D． | （12，0），（-12，0） |
如图所示，某幼儿园有一个游乐场ABCD，其中AB=50米，BC=40米，由于幼儿园招生规模增大，需将该游乐场扩大成矩形区域EFGH，要求A、B、C、D四个点分别在矩形EFGH的四条边（不含顶点）上．设∠BAE=θ（弧度），EF的长为y米．