题目内容
10.已知向量$|{\overrightarrow a}|=4$,$|{\overrightarrow b}|=3$,且$({\overrightarrow a+2\overrightarrow b})•({\overrightarrow a-\overrightarrow b})=4$,则向量$\overrightarrow a$与向量$\overrightarrow b$的夹角为$\frac{π}{3}$.分析 通过向量的数量积的运算,求出角的大小即可.
解答 解:设向量$\overrightarrow a$与向量$\overrightarrow b$的夹角为θ,
∵向量$|{\overrightarrow a}|=4$,$|{\overrightarrow b}|=3$,且$({\overrightarrow a+2\overrightarrow b})•({\overrightarrow a-\overrightarrow b})=4$,
∴${\overrightarrow{a}}^{2}$+$\overrightarrow{a}•$$\overrightarrow{b}$-2${\overrightarrow{b}}^{2}$=${\overrightarrow{a}}^{2}$+|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ-2${\overrightarrow{b}}^{2}$=16+12cosθ-18=4,
即cosθ=$\frac{1}{2}$,
∵0≤θ≤π,
∴θ=$\frac{π}{3}$,
故答案为:$\frac{π}{3}$
点评 本题考查向量的数量积的运算,考查计算能力.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
15.某校高考数学成绩ξ近似地服从正态分布N(100,52),且P(ξ<110)=0.96,则P(90<ξ<100)的值为( )
| A. | 0.49 | B. | 0.48 | C. | 0.47 | D. | 0.46 |
2.某研究机构在对线性相关的两个变量x和y进行统计分析时,得到如下数据:
由表中数据求的y关于x的回归方程为$\hat y=0.65x+\hat a$,则在这些样本点中任取一点,该点落在回归直线下方的概率为( )
| x | 4 | 6 | 8 | 10 | 12 |
| y | 1 | 2 | 3 | 5 | 6 |
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
19.自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,怀化市某学校高三年级为了提高学生自主招生考试的通过率,对A、B、C、D四所国内知名大学2016年自主招生考试的语文和数学的控分做了如下调查:
(Ⅰ)依据上表中的数据用最小二乘法求数学控分$\hat y$关于语文控分x的线性回归方程$\hat y=\hat bx+\hat a$及当某高校自主招生考试语文控分为110分时,预测该校的数学控分.
(Ⅱ)依据调查表,怀化市的这所学校从A、B、C、D四所大学任选两所,求选出的这两所学校的语文和数学控分都低于120分的概率.
(附:线性回归方程$\hat y=\hat bx+\hat a$中,$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}\\ \hat a=\overline y-\hat b×\overline x\end{array}\right.$)
| 学校 | A | B | C | D |
| 语文(x分) | 118 | 120 | 114 | 112 |
| 数学 (y分) | 116 | 123 | 114 | 119 |
(Ⅱ)依据调查表,怀化市的这所学校从A、B、C、D四所大学任选两所,求选出的这两所学校的语文和数学控分都低于120分的概率.
(附:线性回归方程$\hat y=\hat bx+\hat a$中,$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}\\ \hat a=\overline y-\hat b×\overline x\end{array}\right.$)
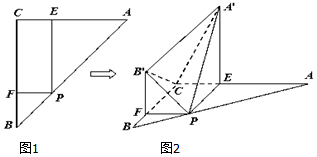 如图,在△ABC中,∠C=90°,AC=BC=a,点P在边AB上,设$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ>0),过点P作PE∥BC交AC于E,作PF∥AC交BC于F.沿PE将△APE翻折成△A′PE,使平面A′PE⊥平面ABC;沿PF将△BPF翻折成△B′PF,使平面B′PF⊥平面ABC.
如图,在△ABC中,∠C=90°,AC=BC=a,点P在边AB上,设$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ>0),过点P作PE∥BC交AC于E,作PF∥AC交BC于F.沿PE将△APE翻折成△A′PE,使平面A′PE⊥平面ABC;沿PF将△BPF翻折成△B′PF,使平面B′PF⊥平面ABC.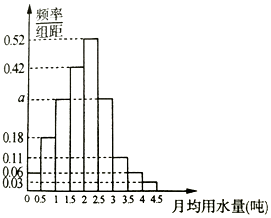 我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超过x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超过x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.