题目内容
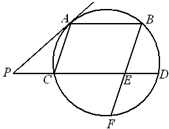 如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.(Ⅰ)求AC的长;
(Ⅱ)试比较BE与EF的长度关系.
考点:相似三角形的性质
专题:选作题,立体几何
分析:(Ⅰ)先求出CE,再证明△PAC∽△CBA,利用相似比,即可求AC的长;
(Ⅱ)由相交弦定理可得CE•ED=BE•EF,求出EF,即可得出结论.
(Ⅱ)由相交弦定理可得CE•ED=BE•EF,求出EF,即可得出结论.
解答:
解:(I)∵过A点的切线交DC的延长线于P,
∴PA2=PC•PD,
∵PC=1,PA=2,
∴PD=4
又PC=ED=1,∴CE=2,
∵∠PAC=∠CBA,∠PCA=∠CAB,
∴△PAC∽△CBA,
∴
=
,
∴AC2=PC•AB=2,
∴AC=
; …(5分)
(II)BE=AC=
,
由相交弦定理可得CE•ED=BE•EF.
∵CE=2,ED=1,
∴EF=
,
∴EF=BE.…(10分)
∴PA2=PC•PD,
∵PC=1,PA=2,
∴PD=4
又PC=ED=1,∴CE=2,
∵∠PAC=∠CBA,∠PCA=∠CAB,
∴△PAC∽△CBA,
∴
| PC |
| AC |
| AC |
| AB |
∴AC2=PC•AB=2,
∴AC=
| 2 |
(II)BE=AC=
| 2 |
由相交弦定理可得CE•ED=BE•EF.
∵CE=2,ED=1,
∴EF=
| 2 |
∴EF=BE.…(10分)
点评:本题考查相似三角形的性质,考查相交弦定理,判断三角形相似是关键.

练习册系列答案
相关题目
直线l:x+y-1006=0分别与函数y=3x和y=log3x的交点为A(x1,y1),B(x2,y2),则2(y1+y2)=( )
| A、2010 | B、2012 |
| C、2014 | D、不确定 |
设a=log2tan70°,b=log2sin25°,c=log2cos25°,则它们的大小关系为( )
| A、a<c<b |
| B、b<c<a |
| C、a<b<c |
| D、b<a<c |