题目内容
10．方程sinπx=|lnx|的解的个数是（ ）| A． | 4 | B． | 8 | C． | 9 | D． | 10 |
分析 分别画出y=sinπx的图象与y=|lnx|的图象，结合图象以及函数的单调性判定出交点的个数即可．
解答 
解：∵函数y=|lnx|，y=sinπx的图象如右图所示：
由图象在[0，1）内有1个交点，x=1时有一个交点，
在（1，$\frac{5}{2}$]内有1个交点，
在（$\frac{5}{2}$，3）内有1个交点，后面y=|lnx|的图象均在y=sinπx图象的上方．
故方程sinπx=|lnx|的根的个数为4个
故选：A．
点评 本题的考点是函数的零点与方程根的关系，主要考查用函数的思想研究方程问题，关键是合理构造函数，充分利用函数的图象，体现了数形结合的思想．属中档题．
练习册系列答案
相关题目
1．若$|{\overrightarrow a}|=1$，$|{\overrightarrow b}|=\sqrt{2}$，（$\overrightarrow{a}$-$\overrightarrow{b}$）•$\overrightarrow{a}$=0，则$\overrightarrow a$与$\overrightarrow b$的夹角为（ ）
| A． | 30° | B． | 45° | C． | 135° | D． | 150° |
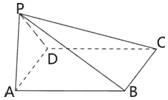如图，平面PAD⊥平面ABCD，ABCD是边长为2的菱形，PA=PD，且∠APD=90°，∠DAB=60°．
5．方程$\frac{6}{x}={log_2}x$的根所在区间是（ ）
| A． | （0，1） | B． | （1，2） | C． | （2，3） | D． | （3，4） |