题目内容
7．半径分别为5，6的两个圆相交于A，B两点，AB=8，且两个圆所在平面相互垂直，则它们的圆心距为$\sqrt{29}$．分析 作出图形，结合图形分别求出两圆圆心到相交弦的距离，由此能求出两圆的圆心距．
解答 解：
如图，半径分别为5，6的两个圆O1，O2相交于A，B两点，AB=8，
两个圆所在平面EFCD⊥平面MNCD，
取AB中点O，连结OO1，OO2，则OO1⊥OO2，
OO1=$\sqrt{{O}_{1}{A}^{2}-O{A}^{2}}$=$\sqrt{25-16}$=3，
OO2=$\sqrt{{O}_{2}{A}^{2}-O{A}^{2}}$=$\sqrt{36-16}$=2$\sqrt{5}$，
∴它们的圆心距|O1O2|=$\sqrt{O{{O}_{1}}^{2}+O{{O}_{2}}^{2}}$=$\sqrt{9+20}$=$\sqrt{29}$．
故答案为：$\sqrt{29}$．
点评 本题考查两圆圆心距的求法，考查推理论证能力、运算求解能力、空间思维能力，考查数形结合思想、转化化归思想，考查运用意识，是中档题．
练习册系列答案
相关题目
17．在△ABC中，角A，B，C所对的边分别为a，b，c，已知cosA=$\frac{1}{3}$．求sin（B+C）的值（ ）
| A． | $\frac{{2\sqrt{2}}}{3}$ | B． | -$\frac{1}{2}$ | C． | 0 | D． | $\frac{3}{4}$ |
15．
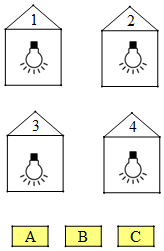如图，A，B，C三个开关控制着1，2，3，4号四盏灯．若开关A控制着2，3，4号灯（即按一下开关A，2，3，4号灯亮，再按一下开关A，2，3，4号灯熄灭），同样，开关B控制着1，3，4号灯，开关C控制着1，2，4号灯．开始时，四盏灯都亮着，那么下列说法正确的是（ ）
如图，A，B，C三个开关控制着1，2，3，4号四盏灯．若开关A控制着2，3，4号灯（即按一下开关A，2，3，4号灯亮，再按一下开关A，2，3，4号灯熄灭），同样，开关B控制着1，3，4号灯，开关C控制着1，2，4号灯．开始时，四盏灯都亮着，那么下列说法正确的是（ ）| A． | 只需要按开关A，C可以将四盏灯全部熄灭 | |
| B． | 只需要按开关B，C可以将四盏灯全部熄灭 | |
| C． | 按开关A，B，C可以将四盏灯全部熄灭 | |
| D． | 按开关A，B，C无法将四盏灯全部熄灭 |
16．已知点P（x，y）的坐标满足x2+y2-2y=0，则$u=\frac{y+1}{x}$的取值范围是（ ）
| A． | $-\sqrt{3}≤u≤\sqrt{3}$ | B． | $u≥\sqrt{3}$或$u≤-\sqrt{3}$ | C． | $-\frac{{\sqrt{3}}}{3}≤u≤\frac{{\sqrt{3}}}{3}$ | D． | $u≥\frac{{\sqrt{3}}}{3}$或$u≤-\frac{{\sqrt{3}}}{3}$ |