题目内容
已知（1-2x）100=a0+a1x+a2x2+…+a100x100，求：
（1）a1+a2+…+a100
（2）a0+a2+a4+…+a100
（3）a1+a3+a5+…+a99
（4）|a0|+|a1|+…+|a100|
（1）a1+a2+…+a100
（2）a0+a2+a4+…+a100
（3）a1+a3+a5+…+a99
（4）|a0|+|a1|+…+|a100|
考点：二项式系数的性质
专题：二项式定理
分析：（1）根据所给的等式可得常数项a0=1，在所给的等式中，令x=1可得a0+a1+a2+a3+…+a100=1，从而求得a1+a2+a3+…+a100的值．
（2）用①加上②再除以2可得 a0+a2+a4+…+a100的值．
（3）在所给的等式中，分别令x=1、x=-1，可得2个等式，化简这2个等式即可求得a1+a3+a5+…+a99的值．
（4）在（1+2x）100中，令x=1，可得|a0|+|a1|+|a2|+…+|a100|的值．
（2）用①加上②再除以2可得 a0+a2+a4+…+a100的值．
（3）在所给的等式中，分别令x=1、x=-1，可得2个等式，化简这2个等式即可求得a1+a3+a5+…+a99的值．
（4）在（1+2x）100中，令x=1，可得|a0|+|a1|+|a2|+…+|a100|的值．
解答：
解：（1）∵已知（1-2x）100=a0+a1x+a2x2+…+a100x100，∴常数项a0=1．
在所给的等式中，令x=1可得a0+a1+a2+a3+…+a100=1，
∴a1+a2+a3+…+a100=0．
（2）在所给的等式中，令x=1可得a0+a1+a2+a3+…+a100=1①，
令x=-1可得得a0-a1+a2-a3+…-a100=3100②，
用①加上②再除以2可得 a0+a2+a4+…+a100=
．
（3）用①减去②再除以2可得 a1+a3+a5+…+a99=
．
（4）在（1+2x）7中，令x=1，可得|a0|+|a1|+|a2|+…+|a100|=3100．
在所给的等式中，令x=1可得a0+a1+a2+a3+…+a100=1，
∴a1+a2+a3+…+a100=0．
（2）在所给的等式中，令x=1可得a0+a1+a2+a3+…+a100=1①，
令x=-1可得得a0-a1+a2-a3+…-a100=3100②，
用①加上②再除以2可得 a0+a2+a4+…+a100=
| 1+3100 |
| 2 |
（3）用①减去②再除以2可得 a1+a3+a5+…+a99=
| 1-3100 |
| 2 |
（4）在（1+2x）7中，令x=1，可得|a0|+|a1|+|a2|+…+|a100|=3100．
点评：本题主要考查二项式定理的应用、二项式展开式的通项公式；求展开式的系数常用的方法是赋值法．
练习册系列答案
相关题目
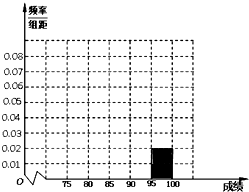某校高三年级在高校自主招生期间，把学生的平时成绩按“百分制”折算并排序，选出前300名学生，并对这300名学生按成绩分组，第一组[75，80），第二组[80，85），第三组[85，90），第四组[90，95），第五组[95，100]，如图为频率分布直方图的一部分，其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列．