题目内容
已知函数f(x)=lnx,g(x)=ax2-x(a≠0).
(1)设F(x)=f(x)-g(x)在[1,+∞)上单调递减,求a的取值范围;
(2)若函数y=f(x)与y=g(x)的图象有两个不同的交点M、N,求a的取值范围;
(3)在(2)的条件下,过线段MN的中点作x轴的垂线分别与f(x)的图象和g(x)的图象交S、T点,以S为切点作f(x)的切线l1,以T为切点作g(x)的切线l2.是否存在实数a使得l1∥l2,如果存在,求出a的值;如果不存在,请说明理由.
(1)设F(x)=f(x)-g(x)在[1,+∞)上单调递减,求a的取值范围;
(2)若函数y=f(x)与y=g(x)的图象有两个不同的交点M、N,求a的取值范围;
(3)在(2)的条件下,过线段MN的中点作x轴的垂线分别与f(x)的图象和g(x)的图象交S、T点,以S为切点作f(x)的切线l1,以T为切点作g(x)的切线l2.是否存在实数a使得l1∥l2,如果存在,求出a的值;如果不存在,请说明理由.
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)由于F(x)=f(x)-g(x)在[1,+∞)上单调递减,可得F′(x)=
-2ax+1≤0在[1,+∞)上恒成立,即a≥
(
+
)在[1,+∞)上恒成立.利用二次函数的单调性求出即可.
(2)由f(x)=g(x)可得lnx=ax2-x,化为a=
(x>0).令h(x)=
,利用导数研究其单调性,求出其极值与最值,数形结合即可得出;
(3)不妨设M(x1,y1),N(x2,y2),且x1>x2,则MN中点的坐标为(
,
).以S、T为切点的切线l1,l2的斜率分别为kS=f′(
)=
,kT=g′(
)=a(x1+x2)-1,假设kS=kT,可得
=y1-y2=lnx1-lnx2,即
=ln
.令
=t>1,可得lnt=
=2-
,令u(t)=lnt+
-2,利用导数研究其单调性即可判断出.
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| x2 |
(2)由f(x)=g(x)可得lnx=ax2-x,化为a=
| lnx+x |
| x2 |
| lnx+x |
| x2 |
(3)不妨设M(x1,y1),N(x2,y2),且x1>x2,则MN中点的坐标为(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| x1+x2 |
| 2 |
| 2 |
| x1+x2 |
| x1+x2 |
| 2 |
| 2(x1-x2) |
| x1+x2 |
2(
| ||
|
| x1 |
| x2 |
| x1 |
| x2 |
| 2(t-1) |
| t+1 |
| 4 |
| t+1 |
| 4 |
| t+1 |
解答:
解:(1)∵F(x)=f(x)-g(x)在[1,+∞)上单调递减,
∴F′(x)=
-2ax+1≤0在[1,+∞)上恒成立,
即a≥
(
+
)在[1,+∞)上恒成立.
令φ(x)=
(
+
),则φ(x)max=φ(1)=1.
∴a的取值范围是a≥1.
(2)由f(x)=g(x)可得lnx=ax2-x,化为a=
(x>0).
令h(x)=
,则h′(x)=
,
当0<x<1时,h′(x)>0,则h(x)单调递增
当x>1时,h′(x)<0,则h(x)单调递减,且
>0.
∴h(x)在x=1处取到最大值h(1)=1,
∴要使y=
与y=a有两个不同的交点,则有0<a<1.
(3)不妨设M(x1,y1),N(x2,y2),且x1>x2,则MN中点的坐标为(
,
).
以S、T为切点的切线l1,l2的斜率分别为kS=f′(
)=
,kT=g′(
)=a(x1+x2)-1,
假设kS=kT,则a(x1+x2)-1=
,
∴a(
-
)-(x1-x2)=
,
∴
=y1-y2=lnx1-lnx2,化为
=ln
.
令
=t>1,可得lnt=
=2-
,
令u(t)=lnt+
-2,u′(t)=
-
=
>0,
∴u(t)在(1,+∞)上单调递增,
∴u(t)>u(1)=0,
∴lnt=
不成立,
因此不存在a使得l1∥l2.
∴F′(x)=
| 1 |
| x |
即a≥
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| x2 |
令φ(x)=
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| x2 |
∴a的取值范围是a≥1.
(2)由f(x)=g(x)可得lnx=ax2-x,化为a=
| lnx+x |
| x2 |
令h(x)=
| lnx+x |
| x2 |
| 1-x-2lnx |
| x3 |
当0<x<1时,h′(x)>0,则h(x)单调递增
当x>1时,h′(x)<0,则h(x)单调递减,且
| lnx+x |
| x2 |
∴h(x)在x=1处取到最大值h(1)=1,
∴要使y=
| lnx+x |
| x2 |
(3)不妨设M(x1,y1),N(x2,y2),且x1>x2,则MN中点的坐标为(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
以S、T为切点的切线l1,l2的斜率分别为kS=f′(
| x1+x2 |
| 2 |
| 2 |
| x1+x2 |
| x1+x2 |
| 2 |
假设kS=kT,则a(x1+x2)-1=
| 2 |
| x1+x2 |
∴a(
| x | 2 1 |
| x | 2 2 |
| 2(x1-x2) |
| x1+x2 |
∴
| 2(x1-x2) |
| x1+x2 |
2(
| ||
|
| x1 |
| x2 |
令
| x1 |
| x2 |
| 2(t-1) |
| t+1 |
| 4 |
| t+1 |
令u(t)=lnt+
| 4 |
| t+1 |
| 1 |
| t |
| 4 |
| (t+1)2 |
| (t-1)2 |
| t(t+1)2 |
∴u(t)在(1,+∞)上单调递增,
∴u(t)>u(1)=0,
∴lnt=
| 2(t-1) |
| t+1 |
因此不存在a使得l1∥l2.
点评:本题考查了利用导数研究函数的单调性极值与最值、导数的几何意义、中点坐标公式、平行线与斜率的关系等基础知识与基本技能方法,考查了等价转化方法、换元法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
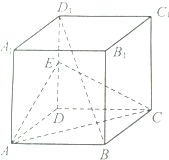 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点.
如图,正方体ABCD-A1B1C1D1中,E为DD1的中点.