题目内容
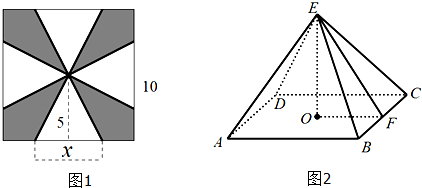
一块边长为10cm 的正方形铁片按如图1所示的阴影部分裁下，然后用余下的四个全等的等腰三角形加工成一个正四棱锥（底面是正方形，从顶点向底面作垂线，垂足是底面的中心的四棱锥）形容器（如图2）．
（1）试把容器的容积V转化为x的函数；
（2）在正四棱锥E-ABCD中，若M是EC的中点，求证AE∥平面BDM．
（1）试把容器的容积V转化为x的函数；
（2）在正四棱锥E-ABCD中，若M是EC的中点，求证AE∥平面BDM．
考点：直线与平面平行的判定,函数解析式的求解及常用方法
专题：计算题,证明题,空间位置关系与距离
分析：（1）用x表示出底面面积和体高，求出体积，（2）连结AC，由线线平行证明线面平行．
解答：
解：（1）正四棱锥的底面边长为x，
体高EO=
=
，
则V=
×x2×
=
x2
（0＜x＜10）．
（2）证明：如图，连结AC，
∵M是EC的中点，O是AC的中点，
∴OM∥AE，
又∵AE?平面BDM，OM?平面BDM；
∴AE∥平面BDM．
体高EO=
| EF2-OF2 |
| 1 |
| 2 |
| 100-x2 |
则V=
| 1 |
| 3 |
| 1 |
| 2 |
| 100-x2 |
| 1 |
| 6 |
| 100-x2 |
（2）证明：如图，连结AC，
∵M是EC的中点，O是AC的中点，
∴OM∥AE，
又∵AE?平面BDM，OM?平面BDM；
∴AE∥平面BDM．
点评：本题考查了空间中线面的位置关系及体积的求法，属于基础题．
练习册系列答案
相关题目
设随机变量ξ～N（0，1），记Φ（x）=P（ξ＜x），则P（-1＜ξ＜1）等于（ ）
| A、2Φ（1）-1 | ||
| B、2Φ（-1）-1 | ||
C、
| ||
| D、Φ（1）+Φ（-1） |
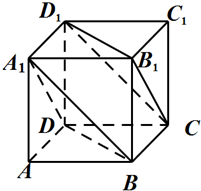如图，在正方体ABCD-A1B1C1D1中．
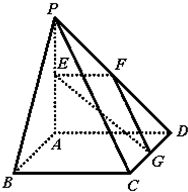如图，四棱锥P-ABCD中，底面ABCD为正方形，PA⊥AD，面PAD⊥面ABCD，PA=AD=2，E，F，G分别是线段PA，PD，CD的中点，