Question

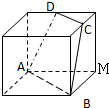如图，正方体的棱长为1，C、D分别是两条棱的中点，A、B、M是顶点，那么点M到截面ABCD的距离是

 

．

Answer 1

考点：点、线、面间的距离计算

专题：计算题,空间位置关系与距离

分析：建立的空间直角坐标系，可得平面ABCD的一个法向量为

n

=（2，-2，1），而M到截面ABCD的距离d=

| AM • n |

| n |

，代入计算即可．

解答： 解：建立如图所示的空间直角坐标系，
可得A（0，0，0），B（1，1，0），D（0，

1

2

，1），M（0，1，0），
∴

AM

=（0，1，0），

AB

=（1，1，0），

AD

=（0，

1

2

，1），
设

n

=（x，y，z）为平面ABCD的法向量，
则

n • AB =x+y=0 n • AD = 1 2 y+z=0

，取y=-2，可得x=2，z=1，
∴

n

=（2，-2，1），
∴M到截面ABCD的距离d=

| AM • n |

| n |

=

2

22+(-2)2+12

=

2

3

故答案为：

2

3

点评：本题考查点到平面的距离，建立坐标系用空间向量来求解是解决问题的关键，属中档题．