题目内容
数列{an}满足a1=1,a2=2,an+2=2an+1-an+2.
(Ⅰ)设bn=an+1-an,证明{bn}是等差数列;
(Ⅱ)求{an}的通项公式.
(Ⅰ)设bn=an+1-an,证明{bn}是等差数列;
(Ⅱ)求{an}的通项公式.
考点:数列递推式,等差数列的通项公式,等差关系的确定
专题:等差数列与等比数列
分析:(Ⅰ)将an+2=2an+1-an+2变形为:an+2-an+1=an+1-an+2,再由条件得bn+1=bn+2,根据条件求出b1,由等差数列的定义证明{bn}是等差数列;
(Ⅱ)由(Ⅰ)和等差数列的通项公式求出bn,代入bn=an+1-an并令n从1开始取值,依次得(n-1)个式子,然后相加,利用等差数列的前n项和公式求出{an}的通项公式an.
(Ⅱ)由(Ⅰ)和等差数列的通项公式求出bn,代入bn=an+1-an并令n从1开始取值,依次得(n-1)个式子,然后相加,利用等差数列的前n项和公式求出{an}的通项公式an.
解答:
解:(Ⅰ)由an+2=2an+1-an+2得,
an+2-an+1=an+1-an+2,
由bn=an+1-an得,bn+1=bn+2,
即bn+1-bn=2,
又b1=a2-a1=1,
所以{bn}是首项为1,公差为2的等差数列.
(Ⅱ)由(Ⅰ)得,bn=1+2(n-1)=2n-1,
由bn=an+1-an得,an+1-an=2n-1,
则a2-a1=1,a3-a2=3,a4-a3=5,…,an-an-1=2(n-1)-1,
所以,an-a1=1+3+5+…+2(n-1)-1
=
=(n-1)2,
又a1=1,
所以{an}的通项公式an=(n-1)2+1=n2-2n+2.
an+2-an+1=an+1-an+2,
由bn=an+1-an得,bn+1=bn+2,
即bn+1-bn=2,
又b1=a2-a1=1,
所以{bn}是首项为1,公差为2的等差数列.
(Ⅱ)由(Ⅰ)得,bn=1+2(n-1)=2n-1,
由bn=an+1-an得,an+1-an=2n-1,
则a2-a1=1,a3-a2=3,a4-a3=5,…,an-an-1=2(n-1)-1,
所以,an-a1=1+3+5+…+2(n-1)-1
=
| (n-1)(1+2n-3) |
| 2 |
又a1=1,
所以{an}的通项公式an=(n-1)2+1=n2-2n+2.
点评:本题考查了等差数列的定义、通项公式、前n项和公式,及累加法求数列的通项公式和转化思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知i是虚数单位,i2=-1,则复数
在复平面上对应点的坐标是( )
| 5i |
| 2-i |
| A、(-1,2) |
| B、(1,-2) |
| C、(1,2) |
| D、(-1,-2) |
正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A、
| ||
| B、16π | ||
| C、9π | ||
D、
|
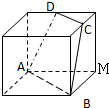 如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是
如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是 如图,设椭圆C:
如图,设椭圆C: