题目内容
李明在10场篮球比赛中的投篮情况统计如下(假设各场比赛相互独立);
(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率;
(2)从上述比赛中随机选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率;
(3)记
是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X为李明在这场比赛中的命中次数,比较EX与
的大小(只需写出结论).
| 场次 | 投篮次数 | 命中次数 | 场次 | 投篮次数 | 命中次数 |
| 主场1 | 22 | 12 | 客场1 | 18 | 8 |
| 主场2 | 15 | 12 | 客场2 | 13 | 12 |
| 主场3 | 12 | 8 | 客场3 | 21 | 7 |
| 主场4 | 23 | 8 | 客场4 | 18 | 15 |
| 主场5 | 24 | 20 | 客场5 | 25 | 12 |
(2)从上述比赛中随机选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率;
(3)记
. |
| x |
. |
| x |
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)根据概率公式,找到李明在该场比赛中超过0.6的场次,计算即可,
(2)根据互斥事件的概率公式,计算即可.
(3)求出平均数和EX,比较即可.
(2)根据互斥事件的概率公式,计算即可.
(3)求出平均数和EX,比较即可.
解答:
解:(1)设李明在该场比赛中投篮命中率超过0.6的概率为事件A,由题意知,李明在该场比赛中超过0.6的场次有:主场2,主场3,主场5,客场2,客场4,共计5场
所以李明在该场比赛中投篮命中率超过0.6的概率P(A)=
=
,
(2)设李明的投篮命中率一场超过0.6,一场不超过0.6的概率为事件B,同理可知,李明主场命中率超过0.6的概率P1=
,客场命中率超过0.6的概率P2=
,
故P(B)=P1×(1-P2)+P2×(1-P1)=
×
+
×
=
;
(3)
=
(12+8+12+12+8+7+8+13+20+12)=11.4
EX=
所以李明在该场比赛中投篮命中率超过0.6的概率P(A)=
| 5 |
| 10 |
| 1 |
| 2 |
(2)设李明的投篮命中率一场超过0.6,一场不超过0.6的概率为事件B,同理可知,李明主场命中率超过0.6的概率P1=
| 3 |
| 5 |
| 2 |
| 5 |
故P(B)=P1×(1-P2)+P2×(1-P1)=
| 3 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 13 |
| 25 |
(3)
. |
| x |
| 1 |
| 10 |
EX=
. |
| x |
点评:本题主要考查了概率的计算、数学期望,平均数,互斥事件的概率,属于中档题.

练习册系列答案
相关题目
已知集合M={y|y=1+
},N={y|y=ln(x2+1)},则M∩N=( )
| 1 | ||
|
| A、(0,+∞) |
| B、[0,+∞) |
| C、(1,+∞) |
| D、[1,+∞) |
正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A、
| ||
| B、16π | ||
| C、9π | ||
D、
|
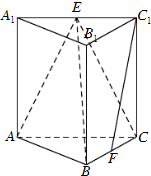 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.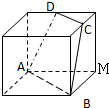 如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是
如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是