题目内容
从正方体六个面的对角线中任取两条作为一对.其中所成的角为60°的共有( )
| A、24对 | B、30对 |
| C、48对 | D、60对 |
考点:排列、组合及简单计数问题,异面直线及其所成的角
专题:排列组合
分析:利用正方体的面对角线形成的对数,减去不满足题意的对数即可得到结果.
解答:
解:正方体的面对角线共有12条,两条为一对,共有
=66条,
同一面上的对角线不满足题意,对面的面对角线也不满足题意,一组平行平面共有6对不满足题意的直线对数,
不满足题意的共有:3×6=18.
从正方体六个面的对角线中任取两条作为一对.其中所成的角为60°的共有:66-18=48.
故选:C.
| C | 2 12 |
同一面上的对角线不满足题意,对面的面对角线也不满足题意,一组平行平面共有6对不满足题意的直线对数,
不满足题意的共有:3×6=18.
从正方体六个面的对角线中任取两条作为一对.其中所成的角为60°的共有:66-18=48.
故选:C.
点评:本题考查排列组合的综合应用,逆向思维是解题本题的关键.

练习册系列答案
相关题目
已知函数f(x)=
-log2x,在下列区间中,包含f(x)零点的区间是( )
| 6 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,4) |
| D、(4,+∞) |
已知i是虚数单位,i2=-1,则复数
在复平面上对应点的坐标是( )
| 5i |
| 2-i |
| A、(-1,2) |
| B、(1,-2) |
| C、(1,2) |
| D、(-1,-2) |
正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A、
| ||
| B、16π | ||
| C、9π | ||
D、
|
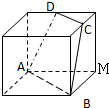 如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是
如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是