题目内容
把5件不同产品摆成一排，若产品A与产品B相邻，且产品A与产品C不相邻，则不同的摆法有 种．
考点：排列、组合的实际应用,排列、组合及简单计数问题
专题：排列组合
分析：分3步进行分析：①用捆绑法分析A、B，②除去A、B相邻又满足A、C相邻的情况．
解答：
解：先考虑产品A与B相邻，把A、B作为一个元素有
种方法，而A、B可交换位置，所以有2
=48种摆法，又当A、B相邻又满足A、C相邻，有2
=12种摆法，故满足条件的摆法有48-12=36种．
故答案为：36．
| A | 4 4 |
| A | 4 4 |
| A | 3 3 |
故答案为：36．
点评：本题考查分步计数原理的应用，要优先分析受到限制的元素，如本题的A、B、C．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
如图，三棱柱ABC-A1B1C1中，侧面BB1C1C为菱形，AB⊥B1C．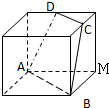
如图，正方体的棱长为1，C、D分别是两条棱的中点，A、B、M是顶点，那么点M到截面ABCD的距离是
已知i是虚数单位，i2=-1，则复数
在复平面上对应点的坐标是（ ）
| 5i |
| 2-i |
| A、（-1，2） |
| B、（1，-2） |
| C、（1，2） |
| D、（-1，-2） |